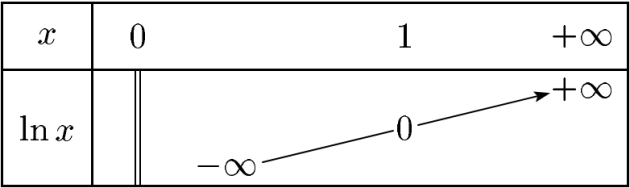
Limites de la fonction ln
Fondamental : Limite en l'infini
\(\lim\limits_{x\to +\infty}\ln x=+\infty\)
Complément : Démonstration
Soit \(A\) un réel strictement positif quelconque.
Si \(x>e^A\), sachant que la fonction \(\ln\) est strictement croissante sur \(]0 ;+\infty[\), on a\( \ln x>\ln e^A\)
Donc si \(x>e^A, ~ \ln x>A\) ce qui est la définition d'une limite infinie en l'infini.
Fondamental : Limite en 0
\(\lim\limits_{x\to 0}\ln x=-\infty\)
Complément : Démonstration
Soit A Un réel strictement négatif quelconque.
Si \(0<x<e^A\), alors \(\ln x<\ln e^A=A\)
On peut donc ainsi rendre la fonction \(\ln\) aussi négative que l'on veut pour peu que l'on s'approche suffisamment de 0
Cela démontre la limite demandée.
Tableau de variation de la fonction ln
On en déduit donc le tableau de variations ci-dessous.
