Étude d'une fonction faisant intervenir ln
On considère la fonction \(f\) définie sur \(]0 ;\pi[\) par \(f(x)=\ln(\sin x)\).
Question
Justifier que \(f\) est bien définie sur \(]0 ;\pi[\).
Indice
\(\ln(u(x)\) est définie si son "contenu" \(u(x)\) est strictement positif.
Solution
Pour que \(f\) soit définie, il faut et il suffit que l'expression qui se trouve à l'intérieur soit strictement positive.
Or l'étude de la fonction Sinus nous révèle que c'est bien le cas sur \(]0 ;\pi[\).
Question
Déterminer les limites de \(f\) aux bornes de son ensemble de définition. En déduire d'éventuelles asymptotes.
Solution
Étude en 0+
\(\lim\limits_{\substack{x \to 0 \\ x>0}} ~\sin x=0^+\) et \(\lim\limits_{\substack{U \to 0 \\ U>0}} ~\ln U=-\infty\)
Donc d'après les théorèmes de composition des limites on en déduit que \(\lim\limits_{\substack{x \to 0 \\ x>0}} ~f(x)=-\infty\).
Étude en π par valeurs inférieures
\(\lim\limits_{\substack{x \to \pi \\ x<\pi}} \sin x=0^+\) et \(\lim\limits_{\substack{U \to 0 \\ U>0}}~ \ln U=-\infty\).
Donc d'après les théorèmes de composition des limites, on en déduit que \(\lim\limits_{\substack{x \to \pi \\ x<\pi}}~ f(x)=-\infty\).
Asymptotes
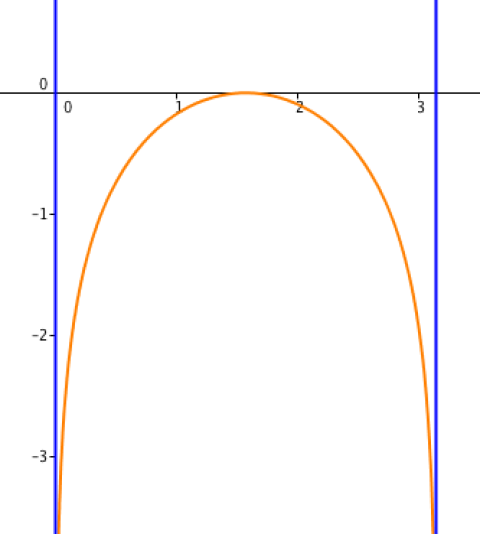
On a donc deux limites infinies en deux points finis, ce qui se traduit par deux asymptotes verticales : une en \(x=0\) et l'autre en \(x=\pi\).
Question
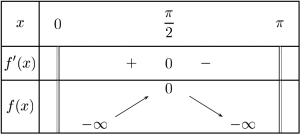
Déterminer le tableau de variations de \(f\) puis sa courbe représentative.