Logarithme décimal : Activité
Le logarithme décimal
Le logarithme décimal, noté \(\log\), est la fonction définie sur \(]0 ;+\infty[\) par
\(\log x=\dfrac{\ln x}{\ln 10}\)
Question
Déterminer \(\log 10\) ; \(\log 100\) ; \(\log 0,001\).
Solution
\(10=10^1\) donc \(\log 10=1\)
\(100=10^2\) donc \(\log 100=2\)
\(0,001=10^{-3}\) donc \(\log 0,001=-3\)
Remarque :
La calculatrice confirme ces résultats en utilisant la formule du log décimal donnée en introduction.

Complément :
De manière générale, on a pour tout entier \(n~ :~\log 10^n=n\)
En effet\( \log 10^n=\dfrac{\ln 10^n}{\ln 10}=\frac{n\ln 10}{\ln 10}=n\)
Question
Démontrer que la fonction \(\log\) est croissante sur \(]0 ;+\infty[\).
Solution
Soient \(0<x<y\) deux réels strictement positifs ordonnées comme indiqué. Montrons que la fonction \(\log\) conserve l'inégalité.
On sait que la fonction \(\ln\) est strictement croissante sur \(]0 ;+\infty[\) donc elle conserve l'inégalité : \(\ln x<\ln y\)
De plus on sait que \(\ln 10 >0\) car \(10>1\). On peut donc diviser par \(\ln 10\) sans changer de sens l'inégalité :
\(\frac{\ln x}{\ln 10}<\frac{\ln y}{\ln 10}\) et donc \(\log x<\log y\)
La fonction \(\log\) conserve les inégalités sur sur \(]0 ;+\infty[\) donc la fonction \(\log\) est croissante sur \(]0 ;+\infty[\).
Question
Sans calculatrice, donner un encadrement entre deux entiers consécutifs des nombres suivants:
\(\log(1789)\) ;\( \log(25665)\) ; \(\log (0.00933)\)
Indice
On pourra utiliser le fait que la fonction \(\log\) est croissante sur \(]0 ;+\infty[\)
Solution
\(1000<1789<10000\). Puisque \(\log\) est croissante, on en déduit que \(3<\log 1789<4\).
De même \(10000<25665<100000\) donc \(4<\log 25665<5\)
Enfin \(0,001<0,00933<0,01\) donc \(-3<\log 0,00933<-2\)
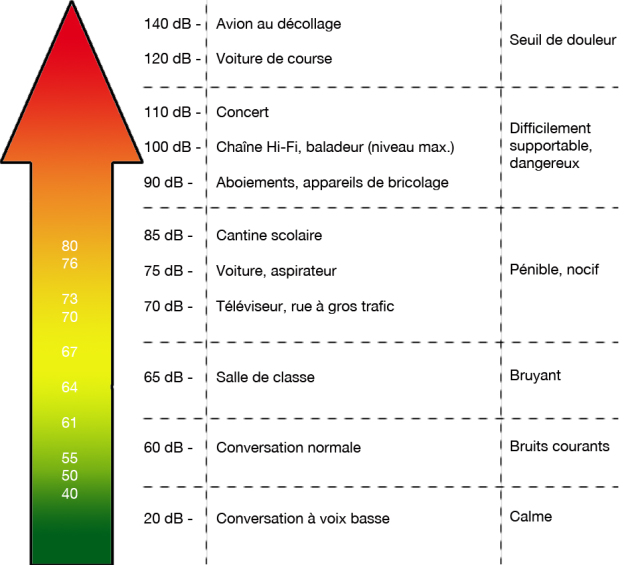
Une application du log décimal : le décibel.

Pour quantifier la sensation sonore, on utilise une grandeur appelée niveau sonore. Cette grandeur, ici notée L, se mesure en décibel acoustique (\(dB_A\))
Le niveau sonore, L, s'exprime en fonction de l'intensité sonore, \(I\), (exprimée en watt par mètre-carré), et de l'intensité sonore de référence, \(I_0\) exprimée dans la même unité que \(I\)
\(L=10\log\left(\dfrac{I}{I_0}\right)\)
Par convention, \(I_0=10^{-12}~ W.m^{-2}\) qui correspond à la limite de sensibilité de l'oreille à la fréquence de 1000 Hz.
Question
Calculer le niveau sonore correspondant à une intensité sonore de \(10^{-5}~W.m^{-2}\) (correspondant au niveau sonore d'un grand magasin à l'heure d'affluence).
Solution
\(L=10\log\frac{10^{-5}}{10^{-12}}=10\log{10^7}=10\times 7=70 ~ dB_A\)
Question
Calculer l'intensité sonore correspondant à un niveau sonore de \(100 ~dB_A\) (marteau piqueur)
Solution
\(10\log\dfrac{I}{I_0}=100\) donc \(\log\dfrac{I}{I_0}=10\) donc \(\dfrac{I}{I_0}=10^{10}\)
Soit \(I=10^{-12}\times 10^{10}=10^{-2}~W.m^{-2}\)
Question
Un réacteur d'avion a un niveau sonore de \(140 ~dB_A\) à environ 100m (niveau qui peut occasionner des lésions irréversibles de l'audition). Quelle est l'intensité sonore correspondante ?
Solution
On procède de la même manière qu'à la question précédente :
\(\dfrac{I}{I_0}=10^{14}\) donc \(I=10^{-12}\times 10^{14}=10^{2}~W.m^{-2}\)
On considère la fonction f définie sur \([10^{-12} ;+\infty[\) par \(f(x)=10\log\frac{x}{10^{-12}}\)
Question
Calculer \(f(10^{-12})\)
Solution
\(f(10^{-12})=\log 1=0\)
Question
Démontrer que pour tout réel \(x\in[10^{-12} ;+\infty[,~~f(x)=10\log x+120\)
Solution
\(f(x)=10\log\frac{x}{10^{-12}}=10(\log x-\log(10^{-12}))=10\log x-10\times (-12)=10\log x+120\)
Question
Calculer \(f'\) et en déduire les variations de f
Solution
\((\log x)'=\left(\dfrac{\ln x}{\ln 10}\right)'=\frac{1}{\ln 10}\times \dfrac{1}{x}\)
\(f'(x)=\dfrac{10}{x\ln 10}\)
Or \(\ln 10>0\) donc \(f'(x)\) est positive sur \([10^{-12} ;+\infty[\) et donc f est croissante sur cet intervalle
Question
Si le niveau sonore passe de \(40~dB_A\) à \(50~dB_A\), l'intensité sonore est multipliée par 10.
Vrai ou Faux ?
Solution
Pour \(40~dB_A\), l'intensité sonore est de \(I=10^{-12}\times 10^{4}=10^{-8}~W.m^{-2}\)
Pour \(50~dB_A\), l'intensité sonore est de \(I=10^{-12}\times 10^{5}=10^{-7}~W.m^{-2}\)
L'intensité a donc été multipliée par 10 lorsqu'on a ajouté \(10~dB_A\)
On a mesuré le niveau sonore de deux machines A et B en fonctionnement. La machine A produit un niveau sonore de \(70~dB_A\) et la machine B produit un niveau sonore de \(80~dB_A\)
On fait fonctionner ces deux machines cote à cote. On admet que dans ce cas, les intensités sonores s'additionnent.
Question
Calculer les intensités sonores de chacune des machines.
Solution
Calculons l'intensité sonore de la machine A :
Pour \(70~dB_A\), l'intensité sonore est de \(I=10^{-12}\times 10^{7}=10^{-5}~W.m^{-2}\)
Calculons l'intensité sonore de la machine B :
Pour \(80~dB_A\), l'intensité sonore est de \(I=10^{-12}\times 10^{8}=10^{-4}~W.m^{-2}\)
Question
Calculer le niveau sonore des deux machines lorsqu'elles fonctionnent ensemble côte à côte.
Que conclure ?
Solution
Additionnons les intensités sonores. On obtient une intensité totale de 0,00011.
Le niveau sonore est donc \(L=10\log 0,00011+120=80,4~dB_A\).
Le fonctionnement de la machine A n'a donc pratiquement aucune influence sur le niveau sonore global.