Utilisation des tables de log
Un peu d'histoire
Nous sommes au 19ème siècle et nous souhaitons rapidement faire l'opération \(232\times 1412\) sans poser la multiplication.
Nous disposons pour cela des tables de logarithmes du livre Bouvart et Ratinet ou alors celles téléchargées sur le site de la BNF. Ici le logarithme utilisé est le logarithme décimal, légèrement différent du logarithme népérien (touche log et non ln sur la calculatrice) mais aux propriétés identiques car proportionnel au logarithme népérien.
Question
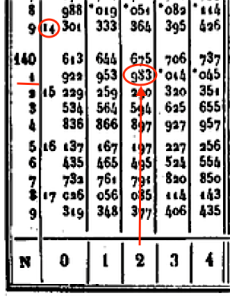
Repérer 232 dans la colonne N. Lire le log qui lui correspond.
Faire de même pour 1412.
Indice
On pourra vérifier sa lecture au moyen de la touche log de la calculatrice - et non ln ! !
Solution
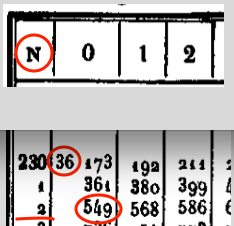
La valeur indiquée dans la table est pour \(2,32\). Or \(232=10^2\times 2,32 = 10 ^2\times 10^{0,36549}=10^{2,36549}\).
Donc \(log 232 \approx 2,36549\).
La valeur indiquée dans la table est pour \(1,412\). Or \(1412=10^3\times 1,412 = 10^3\times 10^{0,14983}=10^{3,14983}\).
Donc \(log 1412 \approx 3,14983\).
Question
Question
En utilisant la table de logarithme, en déduire une valeur approchée de \(232\times 1412\)
Indice
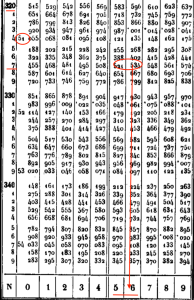
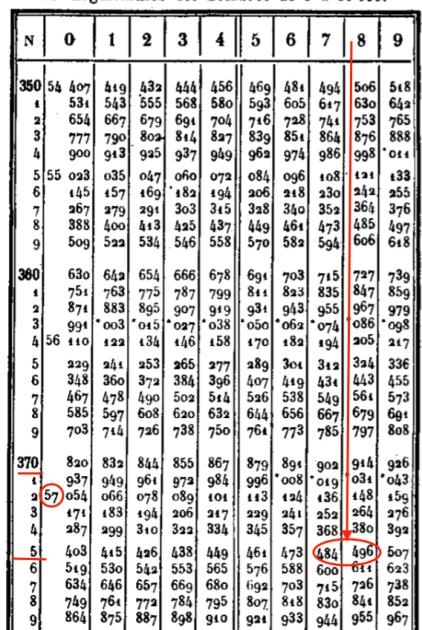
On va lire la table dans l'autre sens et rechercher le nombre dont 0,51532 est le logarithme.
Le nombre exact n’apparaît pas exactement, on obtient donc une approximation du résultat.
Solution
Le nombre qui correspond le mieux dans la table se situe autour de \(3,2758\).
Donc \(232 \times 1412=10^5\times 3,2758=327580\)
On vérifie à la calculatrice ! Et en plus ça marche ... presque. En effet, la valeur 0,51532 n'étant pas dans la table on a choisi un peu au hasard un nombre entre 5 et 6 près de 6 donc 5,8. On obtient en réalité une valeur approchée mais assez exacte. Tout dépend après de la précision des tables de logarithmes. Celles de la BNF sont précises à 7 décimales et auraient donné la valeur exacte à coup sûr.
La même méthodologie peut s'appliquer pour extraire une racine carrée ou élever à une puissance importante. Autant d'opérations très coûteuses à faire à la main et pourtant très courantes dans la vie de tous les jours à l'époque quand on est astronome ou navigateur...
Question
Calculer une valeur approchée de \(\sqrt {1412}\)
Indice
On se rappelle que \(1412=10^{3,14983}\)
Solution
\(\sqrt {1412}=(1412)^{0,5} = 10^{3,14983\times 0,5}=10^{1,57492}=10^1\times 10^{0,57492}\)
On recherche dans la table de logarithmes le nombre \(57~492\)
On obtient \(10^{0,57492} \approx 3,7577\) environ donc \(\sqrt {1412}\approx 10^1\times 3,7578 \approx 37,577\)