Tangentes particulières
Rappel : Équation de la tangente à une courbe en un point a
On se rappelle que l'équation de la tangente à la courbe d'une fonction \(f\) dérivable en un point d'abscisse \(a\) est donnée par la formule :
\(y=f'(a)(x-a)+f(a)\)
Tangente en 1
On a :
\(\ln 1=0\)
\((\ln)'(1)=\dfrac{1}{1}=1\)
\(y=1(x-1)+0\)
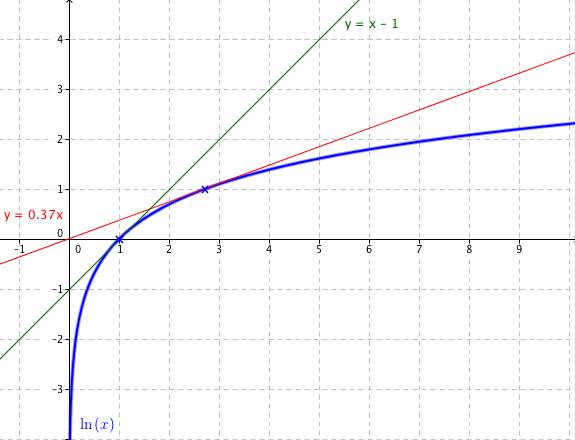
Donc l'équation de la tangente au point d'abscisse 1 a pour équation \(y=x-1\) : le coefficient directeur de la tangente en \(x=1\) vaut 1 et la tangente passe par le point de coordonnées (0 ;-1).
Tangente en e
On a :
\(\ln e=1\)
\((\ln)'(e)=\dfrac{1}{e}\)
\(y=\dfrac{1}{e}(x-e)+1\)
Donc l'équation au point d'abscisse 1 a pour équation \(y=\dfrac{1}{e}x\).
C'est une droite qui passe par l'origine du repère et par le point de coordonnées \((1 ;e)\).
Illustration