Étude de fonction
Étudier la fonction définie sur \(]0 ;+\infty[\) par :
\(f :x \longmapsto 3-x+2\ln x\)
Question
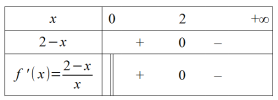
Calculer la dérivée \(f'\) et étudier son signe.
Question
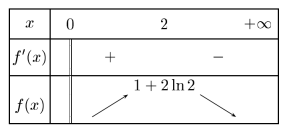
Dresser le tableau de variations de la fonction \(f\).
Solution
D'après la question précédente, on connaît le signe de la dérivée donc les variations de \(f\). Il ne reste qu'à déterminer la valeur de la fonction au point d'abscisse 2 :
\(f(2)=3-2+2\ln 2=1+2\ln 2\approx 2,4\)
Question
Tracer la courbe représentative de la fonction \(f\) avec la calculatrice.
Indice
L'intervalle n'étant pas borné à droite, on pourra se contenter d'aller jusqu'à \(x=5\).
Le tableau de variations montre un maximum en 2,4 environ. On en déduit le réglage de la fenêtre.
Solution

Réglage de la fenêtre d'échelle :
Xmin=0 et Xmax=5
Ymin=-5 et Ymax=2,5