Limite infinie à l'infini
Définition :
Soit \(f\) une fonction définie sur un intervalle \(]a ;+\infty[\).
On dit que f a pour limite \(+\infty\) en \(+\infty\) si les images de \(x\) par la fonction \(f\) prennent des valeurs plus grandes que n'importe quel réel donné dès que \(x\) est assez grand.
On note alors \(\lim\limits_{x \to +\infty} f(x)=+\infty\).
Complément : à titre d'exercice...
On peut donner des définitions analogues d'une :
limite égale à \(-\infty\) en \(+\infty\)
limite égale à \(-\infty\) en \(-\infty\)
limite égale à \(+\infty\) en \(-\infty\)
Exemple : Limites usuelles
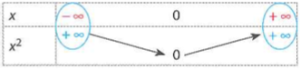
\(\lim\limits_{x \to +\infty} x^2=+\infty\)
\(\lim\limits_{x \to -\infty} x^2 = +\infty\)
\(\lim\limits_{x \to +\infty} \sqrt x=+\infty\)
Complément :
Pour démontrer ces résultats, inspirez-vous de l'activité précédente.
Remarque :
Si une fonction \(f\) admet une limite infinie en \(+\infty\), alors la suite de terme général \(u_n=f(n)\) a la même limite.
Attention :
La réciproque est fausse ! !
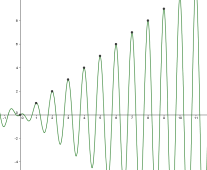
Exemple : \(f(x)=x\sin \left( \frac{\pi}{2}+2\pi x\right)\)
\(f(n)=n\) donc diverge vers \(+\infty\), mais \(f(x)\) oscille sans cesse et n'a pas de limite.
Méthode : Dresser un tableau de variation complet
Dorénavant, on fera figurer dans les tableaux de variations les limites éventuelles.
On lit sur ce tableau que \(\lim\limits_{x \to +\infty} x^2=+\infty\) et \(\lim\limits_{x \to -\infty} x^2=+\infty\)