Limite infinie en un réel
Définition :
Soit f une fonction définie sur un intervalle \(]a ;b[\)
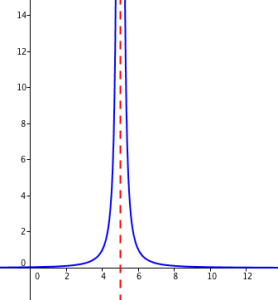
On dit que f tend vers \(+\infty\) quand x tend vers a par valeur supérieure si on peut rendre f(x) aussi grand que l'on veut dès que x est suffisamment proche de a dans l'intervalle \(]a ;b[\)
En d'autres termes, pour tout nombre A, il existe un réel α>0 tel que \(f(x)>A\) dès que \(x\in]a ;a+\alpha[\)
On note \(\lim\limits_{\substack{x \to a \\ x>a}} f(x)=+\infty\)
Complément :
Si la limite par valeur supérieure est égale à la limite par valeur inférieure, on parle simplement de limite lorsque x tend vers a.
Dans l'exemple ci-contre, on a \(\lim\limits_{x \to a } f(x)=+\infty\)
Fondamental : Asymptote verticale
Dans le cas d'une limite infinie en un point d'abscisse finie, on est en présence d'une asymptote verticale à la courbe représentative de la fonction.
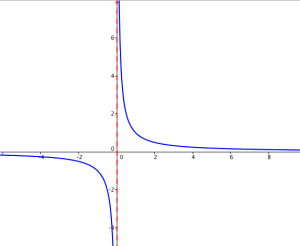
Exemple : Cas de la fonction inverse
On sait que l'inverse d'un nombre positif très petit est très grand, et que ce phénomène s'inverse pour les nombres négatifs. Nous avons donc le résultat suivant :
\(\lim\limits_{\substack{x \to 0 \\ x>0}} \frac{1}{x}=+\infty\)
\(\lim\limits_{\substack{x \to 0 \\ x<0}} \frac{1}{x}=-\infty\)
L'axe des ordonnées est asymptote verticale à la courbe de la fonction inverse.