ROC : Lien entre intégrale et primitive
Soit \(a\) et \(b\) deux réels et \(f\) une fonction continue et positive sur l'intervalle \([a ;b]\).
La fonction \(F(x)=\displaystyle \int_a^x f(t)~dt\) est dérivable sur \([a ;b]\) et a pour dérivée \(f\).
Nous allons démontrer ce théorème dans le cas particulier où \(f\) est en plus croissante sur \([a ;b]\).
Question
Soit \(f\) une fonction continue, positive et croissante sur \([a ;b]\) et \(F(x)=\displaystyle \int_a^x f(t)~dt\).
Soit \(x_0\in [a ;b]\) et h un réel tel que \(x_0+h\in[a ;b]\).
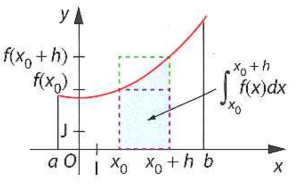
Montrer que si \(h>0\), \( f(x_0)\leqslant \frac{F(x_0+h)-F(x_0)}{h}\leqslant f(x_0+h)\).
Solution
Si h>0
\(F(x_0+h)-F(x_0)\) désigne l'aire sous la courbe comprise entre \(x_0\) et \(x_0+h\).
Puisque f est croissante, cette aire est comprise entre :
l'aire du rectangle sous la courbe de base h et de hauteur \(f(x_0)\) soit \(h\times f(x_0)\),
et l'aire du rectangle au dessus la courbe de base h et de hauteur \(f(x_0+h)\) soit \(h\times f(x_0+h)\).
Par conséquent, on a l'inégalité :
\(hf(x_0)\leqslant F(x_0+h)-F(x_0) \leqslant hf(x_0+h)\)
Puisque \(h>0\), on peut diviser cette inégalité par \(h\) pour obtenir l'inégalité demandée.
Question
Montrer que si \(h<0\), \(f(x_0+h)\leqslant \frac{F(x_0+h)-F(x_0)}{h}\leqslant f(x_0)\).
Solution
Si h<0
\(F(x_0)-F(x_0+h)\) désigne l'aire sous la courbe comprise entre \(x_0+h\) et \(x_0\).
Puisque \(f\) est croissante, cette aire est comprise entre :
l'aire du rectangle sous la courbe de base \(-h\) et de hauteur \(f(x_0+h)\) soit \(-h\times f(x_0+h)\),
et l'aire du rectangle au dessus la courbe de base \(-h\) et de hauteur \(f(x_0)\) soit \(-h\times f(x_0)\).
Par conséquent, on a l'inégalité :
\(-hf(x_0+h)\leqslant F(x_0)-F(x_0+h) \leqslant -hf(x_0)\)
Puisque \(h<0\), on peut diviser cette inégalité par \(-h>0\) pour obtenir :
\(f(x_0+h)\leqslant \dfrac{F(x_0)-F(x_0+h)}{-h} \leqslant f(x_0)\)
En multipliant par -1 le numérateur et le dénominateur de \(\dfrac{F(x_0)-F(x_0+h)}{-h}\), on obtient l' inégalité demandée.
Question
En déduire que \(F\) est dérivable en \(x_0\) et que \(F'(x_0)=f(x_0)\).
Solution
Nous savons que si \(x_0\in [a ;b]\) et \(x_0+h\in[a ;b]\).
Alors \(f(x_0)\leqslant \frac{F(x_0+h)-F(x_0)}{h}\leqslant f(x_0+h)\) ou \(f(x_0+h)\leqslant \dfrac{F(x_0)-F(x_0+h)}{-h} \leqslant f(x_0)\) selon le signe de \(h\).
Si \(h>0\), faisons tendre \(h\) vers 0 dans cette inégalité, par valeurs positives :
\(f(x_0)\) est constant donc tend vers \(f(x_0)\).
\(f(x_0+h)\) tend vers \(f(x_0)\) car la fonction \(f\) est continue en \(x_0\). On utilise ici la définition de la continuité en \(x_0\)
D'après le théorème des gendarmes, on en déduit que \(\dfrac{F(x_0+h)-F(x_0)}{h}\) converge "à droite" vers une limite et que cette limite est \(f(x_0)\).
On obtient donc que \(\lim\limits_{\substack {h \to 0\\ h>0}} \dfrac{F(x_0+h)-F(x_0)}{h} =f(x_0)\).
Par l'autre inégalité et le même principe, on obtient que la limite à gauche du quotient vaut aussi \(f(x_0)\) :
\(\lim\limits_{\substack {h \to 0\\ h<0}} \dfrac{F(x_0+h)-F(x_0)}{h} =f(x_0)\)
Par égalité de la limité à gauche et de la limite à droite, on peut affirmer que la limite existe en 0 et qu'elle vaut \(f(x_0)\) :
\(\lim\limits_{h \to 0} \dfrac{F(x_0+h)-F(x_0)}{h} =f(x_0)\)
Mais d'après la définition du nombre dérivé d'une fonction en un point cette limite est aussi \(F'(x_0)\).
On vient donc de montrer que \(F\) est dérivable en \(x_0\) et que \(F'(x_0)=f(x_0)\).
Nous avons donc démontré le théorème fondamental reliant intégrales et primitives dans le cas particulier d'une fonction croissante.
Ce théorème reste vrai dans le cas d'une fonction non monotone sur un intervalle [a ;b].