Activité algorithmique
Nous cherchons dans cette activité à améliorer la précision du calcul de l'aire précédente. Pour ce faire, nous allons utiliser un algorithme que nous pourrons programmer sur ordinateur ou calculatrice.
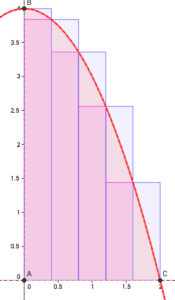
On considère la fonction \(f :x\longmapsto 4-x^2\) définie, continue et positive sur l'intervalle \([0 ;2]\).
On sépare l'intervalle \([0 ;2]\) en n intervalles de longueur \(\dfrac{2}{n}\) chacun : \(\left[0 ;\dfrac{2}{n}\right]~\left[\dfrac{2}{n} ;\dfrac{4}{n}\right]~\ldots ~\left[k\dfrac{2}{n} ;(k+1)\dfrac{2}{n}\right]~\ldots ~\left[{(n-1)\dfrac{2}{n} ;2}\right]\)
On appelle \(S_1\) la somme des rectangles sous la courbe s'appuyant sur les \(n\) intervalles définis ci-dessus.
On appelle \(S_2\) la somme des rectangles sur la courbe s'appuyant sur les \(n\) intervalles définis ci-dessus.
L'activité précédente montre à l'aide de GeoGebra que pour \(n=250\), \(S1\approx 5,32\) et \(S_2\approx 5,35\).
Question
Soit \(k\) un entier compris entre 0 et \((n-1)\).
On considère l'intervalle \(\left[k\dfrac{2}{n} ;(k+1)\dfrac{2}{n}\right]\).
En s'appuyant sur la construction précédente, sur cet intervalle,
quelle est l'aire du rectangle situé sous la courbe ?
quelle est l'aire du rectangle situé sur la courbe ?
Indice
La fonction \(f\) est décroissante sur \([0 ;2]\)
Solution
La fonction \(f\) est décroissante sur \([0 ;2]\) donc pour tout \(x\in \left[k\dfrac{2}{n} ;(k+1)\dfrac{2}{n}\right]\), \(f(k+1)\dfrac{2}{n}\leqslant f(x)\leqslant k\dfrac{2}{n}\).
De plus, chaque rectangle a pour base \(\dfrac{2}{n}\) donc
l'aire du rectangle sous la courbe est \(f\left((k+1)\dfrac{2}{n}\right)\times \dfrac{2}{n}\),
l'aire du rectangle sur la courbe est \(f\left(k\dfrac{2}{n}\right)\times \dfrac{2}{n}\).
Question
Écrire un algorithme prenant en entrée le nombre \(n\) de subdivisions de l'intervalle \([0 ;2]\) et affichant en sortie les valeurs de \(S_1\) et \(S_2\) ainsi que la largeur de l'encadrement de l'aire obtenu.
Indice
On pourra utiliser deux variables S1 et S2 pour stocker les sommes recherchées.
Indice
Une boucle pour semble bien adaptée car on sait dès le départ le nombre \(n\) d'itérations nécessaires.
Solution
INITIALISATION:
Saisir n
S1 prend la valeur 0
S2 prend la valeur 0
TRAITEMENT :
Pour k allant de 0 à n-1 Faire :
S1 prend la valeur S1 + 2/n*f(2*(k+1)/n)
S2 prend la valeur S2 + 2/n*f(2*k/n)
Fin Pour
SORTIE :
Afficher S1, S2 et S2-S1
Question
Programmer cet algorithme sur calculatrice ou ordinateur et retrouver les résultats donnés par GeoGebra.
Solution
Voici le programme sous Python. Sur calculatrice, le programme est très semblable. Il faut toutefois faire attention à renommer les variables s1 et s2 en R et S par exemple car les calculatrices n’acceptent en général que des noms d'une lettre.
def f(x):
return 4-x*x
s1,s2=0,0
n=int(input("Entrer n : "))for k in range(n):
s1=s1+2/n*f(2*(k+1)/n)
s2=s2+2/n*f(2*k/n)
print(s1)
print(s2)
print(s2-s1)
Question
En utilisant votre programme, donner une valeur approchée à \(10^{-2}\) de la valeur de l'aire sous la courbe \(\mathcal C_f\) entre \(x=0\) et \(x=2\)
Solution
En prenant n=1000, le programme retourne :
s1=5.329332000000006
s2=5.337332000000005
une précision de l'encadrement de \(s2-s1\approx 0.008\)
On en déduit que 5,33 est une valeur approchée à \(10^{-2}\) qui convient.