Seconde méthode pour calculer une intégrale
On définit \(f :x\longmapsto 2x-3\).
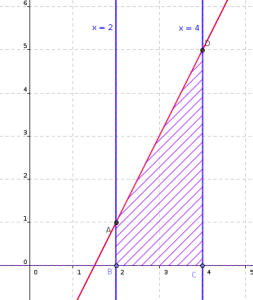
On cherche à calculer \(\displaystyle \int_2^4 2x-3~dx\) en utilisant le théorème vu au paragraphe précédent.
Question
Chercher une fonction \(F(x)\) dont \(f(x)\) est la dérivée.
Indice
On pourra chercher dans la famille des polynômes du second degré car la dérivée d'un polynôme du second degré est une fonction affine.
Solution
On sait que \(2x\) est la dérivée de \(x^2\) et que \(3\) est la dérivée de \(3x\). On peut proposer comme fonction \(F(x)=x^2-3x\). \(F'(x)=2x-3=f(x)\)
Attention :
Cette fonction F n'est pas unique. En effet, on sait qu'une constante se dérive en 0. On peut donc ajouter à \(F(x)\) n'importe quelle constante, on aura toujours\( F'(x)=f(x)\). On aurait ainsi pu prendre \(F(x)=x^2-3x+10\)
Question
En déduire la valeur de \(\displaystyle \int_2^4 2x-3~dx\)
Indice
On se rappelle que si on connaît une fonction \(F\) dérivable dont la dérivée est \(f\), nous avons \(\displaystyle \int_a^b f(t)~dt=F(b)-F(a)\).
Solution
On connaît \(F(x)=x^2-3x\) qui est dérivable et \(F'(x)=f(x)\). Par conséquent \(\displaystyle \int_{-2}^4 2x-3~dx=F(4)-F(2)\). Or
\(F(4)=16-12=4\)
\(F(2)=4-6=-2\)
Donc \(\displaystyle \int_{-2}^4 2x-3~dx=4-(-2)=6\).
Cela se vérifie aisément sur le graphique en comptant les carreaux.
Complément :
Si on avait utilisé une autre fonction \(F\) différente de la première par une constante, le résultat eut été le même. Par exemple si on prend \(F(x)=x^2-3x+10\), on a :
\(F(2)=8\)
\(F(4)=14\)
donc \(\displaystyle \int_{-2}^4 2x-3~dx=14-8=6\).
Peu importe donc la fonction \(F\) choisie du moment que l'on a \(F'=f\).