Notion d'intégrale
Soit (O,I,J) un repère orthogonal du plan. L'unité d'aire est l'aire du rectangle OIKJ comme indiqué sur la figure ci-contre.
Définition : Intégrale d'une fonction
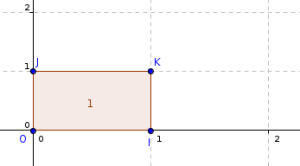
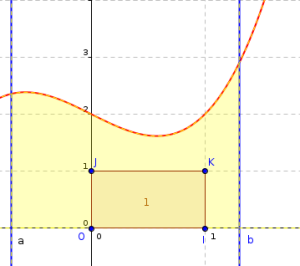
Soit a et b deux réels et f une fonction continue et positive sur l'intervalle \([a ;b]\). \(\mathcal C\) désigne sa courbe représentative dans un repère orthogonal (O,I,J)
L'intégrale de \(f\) entre \(a\) et \(b\) est l'aire, en unité d'aire, du domaine compris entre la courbe \(\mathcal C\), l'axe des abscisses et les droites d'équation \(x=a\) et \(x=b\).
On note ce nombre \(\displaystyle \int_a^b f(x)~dx\)
Exemple :
Dans l'exemple de l'activité, on peut dire que \(5,32<\displaystyle \int_0^2 4-x^2~dx<5,35\)
Remarque :
Dans la notation intégrale, la variable \(x\) peut être remplacée par n'importe quelle lettre : \(\displaystyle \int_a^b f(x)~dx\) équivaut à \(\displaystyle \int_a^b f(t)~dt\) ou encore \(\displaystyle \int_a^b f(u)~du\)
Le symbole \(\displaystyle \int\) a été introduit par Leibniz au XVIIè siècle. Il représente un \(\mathcal S\) stylisé, faisant référence à la Somme de tous les petits rectangles utilisés dans l'activité pour approcher l'aire sous la courbe.