Utiliser la calculatrice pour calculer une intégrale
Reprenons l'exemple de l'activité précédente et calculons à l'aide de la calculatrice la valeur de \(\displaystyle \int_0^2 4-x^2~dx\)
Sur calculatrice TI
Méthode :
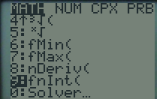
La fonction intégrale se trouve dans le menu \(\fbox{MATH}\) sous la dénomination fnInt(
Les arguments à passer à la fonction fnint( sont dans l'ordre
la fonction
la variable (X en général)
la première borne de l'intervalle (a)
la seconde borne de l'intervalle (b)
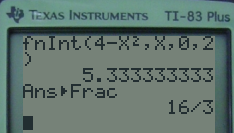
On obtient donc \(\displaystyle \int_0^2 4-x^2~dx=\dfrac{16}{3}\)
Sur calculatrice Casio
Méthode :
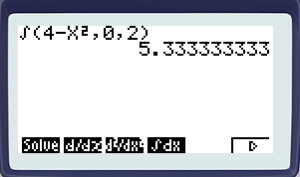
La fonction intégrale se trouve en mode calcul dans le menu \(\fbox{OPTN}\) / \([CALC]\) / \([ \int ~dx]\) (à coté de la fonction dérivée).
Les arguments à passer à la fonction sont dans l'ordre
la fonction
la première borne de l'intervalle (a)
la seconde borne de l'intervalle (b)
On obtient donc \(\displaystyle \int_0^2 4-x^2~dx\approx 5,33\)