Théorèmes de comparaison
Les théorèmes suivants sont très pratiques pour calculer une limite d'une fonction compliquée en la comparant à des fonctions plus simples dont on connaît la limite.
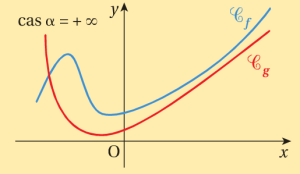
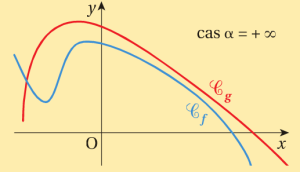
Fondamental : Théorème de comparaison
Soit \(f\) et \(g\) deux fonctions définies sur un intervalle \(I\) voisinage de α, α étant un réel, \(+\infty\) ou \(-\infty\)
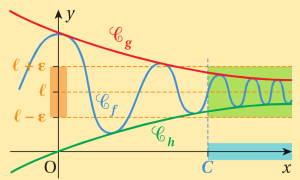
Fondamental : Théorème des gendarmes
Soit \(f\) , \(g\) et \(h\) trois fonctions définies sur un intervalle \(I\) voisinage de α, α étant un réel, \(+\infty\) ou \(-\infty\)