Dérivée en un point
Définition :
Si le quotient \(T_a(h)=\frac{f(a+h)-f(a)}{h}\) tend vers un nombre réel lorsque h tend vers 0, alors on dit que f est dérivable en a.
Le nombre réel vers lequel tend le taux d'accroissement \(T_a(h)\) est appelé nombre dérivé de f en a. On le note \(f'(a)\).
Remarque :
En reprenant la notation des limites introduite lors de l'exercice précédent, on peut écrire :
\(f'(a)=\lim\limits_{h\to0} \frac{f(a+h)-f(a)}{h}\)
Le nombre h s'étant rapproché de 0, le nombre dérivé \(f'(a)\) ne dépend plus que de a contrairement au taux d'accroissement \(T_a(h)\) qui dépend à la fois de a et de h. C'est la différence fondamentale qu'il y a entre le taux d'accroissement et le nombre dérivé : le second étant la limite du premier lorsque \(h\) tend vers 0.
Exemple :
En reprenant l'exercice du paragraphe précédent, on peut affirmer avec les notations introduites ici que \(f :x\longmapsto x^2\) est dérivable en 2 et \(f'(2)=4\).
Complément : Utiliser la calculatrice Casio pour calculer f'(a)
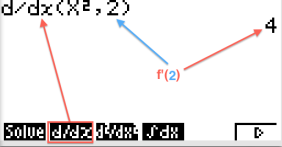
Pour calculer la dérivée en un point avec une calculatrice de type CASIO, aller dans MENU RUN OPTN CALC.
On calcule ici la dérivée en 2 de la fonction \(f(x)=x^2\), c'est à dire \(f'(2)\).
Complément : Utiliser la calculatrice TI pour calculer f'(a)

Pour calculer la dérivée en un point avec une calculatrice de type TI, aller dans MATH8 :nDeriv(.
On calcule ici la dérivée en 2 de la fonction \(f(x)=x^2\), c'est à dire \(f'(2)\).