Définition

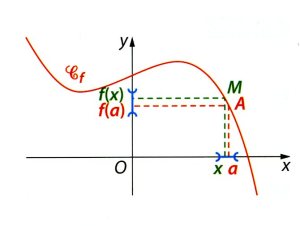
Soit une fonction \(f\) définie sur un intervalle \(I\) et un réel \(a\in I\). On note \(\mathcal C_f\) la courbe représentative de \( f\) et \(A\) le point de \(\mathcal C_f\) d'abscisse \(a\). Pour tout réel \(x\in I\), on considère le point M de \(\mathcal C_f\) d'abscisse \(x\).

En général, lorsque la courbe \(\mathcal C_f\) est "sans trous", c'est à dire qu'on peut la parcourir sans lever le crayon, lorsque le nombre x est proche du nombre a, le point M est également proche du point A.

On dit alors que la fonction est continue sur l'intervalle I. Nous allons formaliser cette notion de manière un peu plus rigoureuse en nous aidant de la notion de limite vue au chapitre précédent.

DéfinitionDéfinition rigoureuse de la continuité

Soit une fonction \(f\) définie sur un intervalle \(I\).

On dit que la fonction \(f\) est continue en un réel \(a\in I\) si \(\lim\limits_{x \to a} f(x)=f(a)\), c'est-à-dire si \(\lim\limits_{\substack {x \to a\\ x<a}} ~f(x)=f(a)\) et \(\lim\limits_{\substack {x \to a\\ x>a}} ~f(x)=f(a)\)

On dit que la fonction \(f\) est continue sur un intervalle I si \(f\) est continue pour tout réel \(a\in I\).

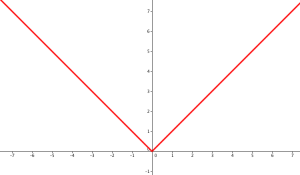
ExempleFonction valeur absolue

On définit la fonction valeur absolue sur \(\mathbb{R}\) par :

  • \(V(x)=x\) si \(x≥0\)

  • \(V(x)=-x\) si \( x<0\)

Cette fonction se représente par deux demi-droites qui se joignent en 0. Sa courbe représentative forme un « V » assez reconnaissable.

Cette fonction est définie pour tout réel et est continue sur \(\mathbb{R}\) car même en 0 où se produit un changement de forme, on peut ne pas lever le crayon lors du tracé.

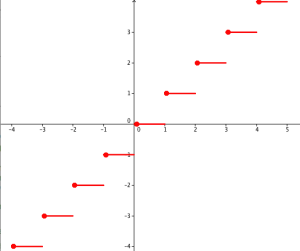
ExemplePartie entière

On définit la fonction partie entière sur \(\mathbb{R}\) par \(x\longmapsto E(x)\) où E(x) est le plus grand entier inférieur ou égal à x. Ainsi :

  • E(2,5)=2

  • E(-2,4)=-3

  • E(1,9999999)=1

  • E(2)=2

La fonction partie entière n'est pas continue pour chaque valeur de x entière. Elle forme ce qu'on appelle une fonction en escalier.

Elle est par contre continue sur « chaque marche », c'est à dire sur chaque intervalle \([n ;n+1[\) où \(n\in \mathbb{N}\). Pour chaque valeur entière, un gros point sur la courbe indique la valeur effectivement prise par la fonction pour éviter toute ambiguïté de lecture graphique.

On voit sur cet exemple par exemple que :

  • \(\lim\limits_{\substack{x \to 1 \\ x>1}} ~E(x)=2\)

  • \(\lim\limits_{\substack{x \to 1 \\ x<1}} ~E(x)=1\)

  • \(E(1)=1\)

Par conséquent, la limite en 1 n'existe pas (il y a une limite à droite et une à gauche). On ne peut pas écrire \(\lim\limits_{x \to 1} E(x)=E(1)\) donc la fonction n'est pas continue en 1 et il en est de même pour chaque entier.