Forme trigonométrique
La propriété suivante se justifie aisément par les propriétés des symétries axiale et centrale.
Fondamental :
\(|\overline z|=|z|\) et si \(z\neq 0\), alors \(\arg(\overline z)=-\arg (z)~(2\pi)\).
\(|-z|=|z|\) et si \(z\neq 0 \), alors \(\arg(-z)=\arg (z)+\pi~~~(2\pi)\)
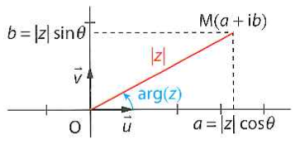
Fondamental : Forme trigonométrique d'un complexe
Soit \(z=a+ib\) un complexe non nul et \(\theta\) un argument de \(z\).
Alors \(a=|z| \cos \theta\) et \(b=|z| \sin \theta\).
L'écriture \(z=|z| (\cos\theta + i\sin\theta)\) est appelée forme trigonométrique de \(z\).
Complément : Démonstration
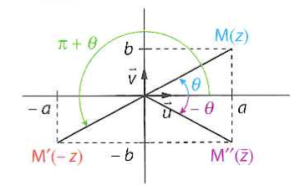
Considérons le point \(M_1\) du cercle trigonométrique défini par \(\overrightarrow{OM_1}=\frac{1}{OM} \overrightarrow{OM}\)
Les vecteurs \(\overrightarrow{OM_1}\) et \(\overrightarrow{OM}\) sont colinéaires de même sens, donc l'angle orienté \((\vec u ;\overrightarrow{OM_1})\) est égal à l'angle orienté \((\vec u ;\overrightarrow{OM})\)
Par conséquent les coordonnées de \(M_1\) sur le cercle trigonométrique sont \((\cos \theta ;\sin \theta)\)
Si \(z_1\) est l'affixe de \(M_1\), on a \(z_1=\cos\theta +i\sin\theta\)
Mais on a \(z_1=\frac{z}{|z|}\) donc \(z=|z| \times ~~z_1\)
Donc \(z=|z| (\cos\theta + i\sin\theta)\).
Exemple :
Soit \(z=\sqrt 3+i\).
On a \(|z| =\sqrt{3+1}=2\).
Donc \(z=2\left(\frac{\sqrt 3}{2}+\frac{1}{2}i\right)\)
On reconnaît entre les parenthèses \(\cos\frac{\pi}{6}\) et \(\sin\frac{\pi}{6}\).
Donc \(z=2\left(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)\) est la forme trigonométrique de \(z\)
On en déduit que \(\arg(z)=\frac{\pi}{6}~(2\pi)\).
Complément : Égalité de deux complexes
Deux complexes non nuls sont égaux si et seulement si ils ont le même module et le même argument modulo \(2\pi\).