Propriétés des modules
Fondamental :
Soit \(z\) et \(z'\neq 0\) deux complexes. Alors :
Module du conjugué : \(| \overline z| = | z|\)
Module d'un produit : \(| z z'|=| z|\times | z'|\)
Module d'un quotient : \(\left| \dfrac{z}{z'}\right|=\dfrac{| z|}{| z'|}\)
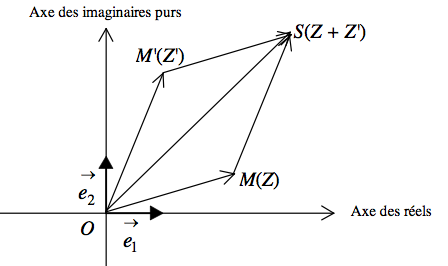
Inégalité triangulaire : \(| z+z'|\leqslant | z| +| z'|\)
Complément : Démonstration
\(| \overline z|^2 =\overline z \left(\overline{ \overline z}\right)=\overline z z=| z| ^2\) ce qui donne la première égalité puisque le module est positif.
\(| z z'|^2=zz'\overline{zz'}=\left(z\overline z \right)z' \overline {z'}=| z| ^2 |z'| ^2\)
Puisqu'un module est positif, on en déduit que \(| zz'|=| z| | z'|\).
On procède de manière analogue pour le quotient.
L'inégalité triangulaire se justifie aisément grâce à la figure ci-dessous.