Introduction à la loi exponentielle
Étude d'une situation
Une entreprise fabriquant des téléviseurs a effectué un suivi de la première panne des appareils qu'elle a fabriqués et vendus.
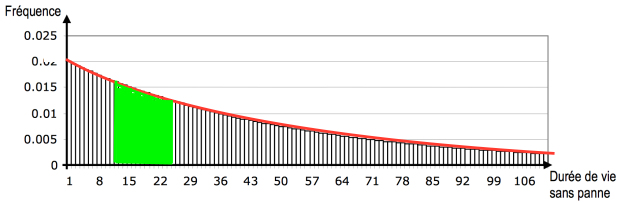
On a réalisé ci-dessous un histogramme résumant les résultats (on a porté en abscisses la durée en mois et en ordonnées la fréquence). Les classes ont une amplitude de 1 mois.
Par exemple, 1,5% des appareils vendus ont subi leur première panne 16 mois après leur achat par le client.
Question
On note T la variable aléatoire donnant l'instant (exprimé en mois) de la première panne d'un téléviseur.
Exprimer par une phrase simple la probabilité \(\mathbb P(T\geqslant t)\).
Expliquer pourquoi T est une variable aléatoire à densité (loi continue). Quelles sont les valeurs possibles prises par T ?
En déduire \(\mathbb P(T\geqslant 0)\).
Solution
\(\mathbb P(T\geqslant t)\) désigne la probabilité que le téléviseur soit encore en fonctionnement au bout de \(t\) mois.
Le téléviseur ne va pas tomber en panne systématiquement le 1er jour du mois, mais à tout moment, par exemple au bout de 19 mois, 6 jours, 3 heures et 48 secondes.... \(T\) peut donc prendre n'importe quelle valeur réelle dans l'intervalle \([0 ;+\infty[\).
On suppose que quand on sort le téléviseur du carton, il est en état de fonctionnement - il a été vérifié en usine. Par conséquent la probabilité qu'il fonctionne est égale à 1 :
\(\mathbb P(T\geqslant 0)=1\)
Dans la suite, on cherche à déterminer la fonction densité associée à la variable aléatoire T.
Question
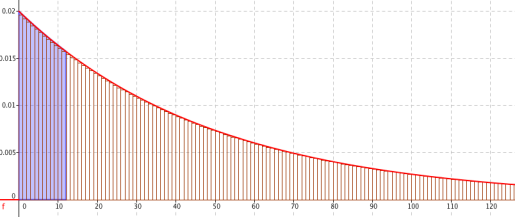
Tracer en rouge sur le graphique la fonction densité associée à la variable aléatoire T.
Tracer en vert ce qui correspond à la probabilité que le téléviseur tombe en panne au cours de la 2eme année.
Question
Le fichier ci-dessous donne les chiffres de l'enquête statistique relatifs au graphique donné dans l'exercice. A l'aide du tableur, déterminer la fonction densité associée à la variable aléatoire T.
Indice
On pourra utiliser la courbe de tendance.
Solution
Utilisation de la courbe de tendance
On constate sur le tableur que la fonction rejoignant au mieux les points a pour expression environ\(f(x)=0,02e^{-0,02x}\).
Question
Soit \(f(x)=0,02e^{-0,02x}\). Démontrer que cette fonction est bien une fonction densité de probabilité sur l'intervalle \([0 ;+\infty[\).
Indice
Pour calculer \(\displaystyle \int_0^{+\infty} f(t)~dt\), on pourra déterminer \(\lim\limits_{x \to +\infty} \displaystyle \int_0^xf(t)~dt\)
Solution
Montrons que la fonction \(f\) est une fonction de densité :
\(f\) est continue et positive sur \([0 ;+\infty[\)
Calculons \(\displaystyle \int_0^xf(t)~dt=\displaystyle \int_0^x 0,02e^{-0,02t}~dt=\left[-e^{-0,02t}\right]_0^x=1-e^{-0,02x}\)
Donc \(\lim\limits_{x \to +\infty} \displaystyle \int_0^xf(t)~dt=\lim\limits_{x \to +\infty} 1-e^{-0,02x}=1\)
Ce qui démontre que la fonction f est bien une fonction densité de probabilité sur l'intervalle \([0 ;+\infty[\).
Fonction densité de probabilité de T
Dans la suite du problème, on considérera que la fonction \(f : x \longmapsto 0,02e^{-0,02x}\) est la fonction densité associée à la variable aléatoire T.
Question
Le téléviseur est garanti un an. Calculer la probabilité qu'il tombe en panne lors de sa période de garantie.
Quelle est la probabilité que le téléviseur fonctionne encore au bout d'un an ?
Solution
\(\mathbb P(T < 12)=\displaystyle \int_0^{12}0,02e^{-0,02x} dx=\left[-e^{-0,02x}\right]_0^{12}\approx 0,2133\)
On peut donc s'attendre à une probabilité de panne de 21% la première année. La probabilité de tomber en panne sous garantie est donc de \(\frac 1 5\).
"Le téléviseur fonctionne encore au bout d'un an" est l'événement contraire de "Le téléviseur est tombé en panne la première année".
Par conséquent la probabilité recherchée est \(\mathbb P(T\geqslant 12)=1-(1-e^{-0,24})=e^{-0,24}\approx 0,7866\).
Question
Calculer la probabilité que le téléviseur tombe en panne entre la première année et la seconde année.
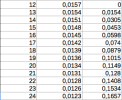
Vérifier votre réponse à l'aide du fichier tableur en reprenant les données de l'étude statistique.
En déduire la probabilité que le téléviseur fonctionne encore au bout de 2 ans.
Solution
Calculons \(\mathbb P(12\leqslant T\leqslant 24) = \displaystyle \int_{12}^{24} 0,02e^{-0,02t}~dt=\left[-e^{-0,02t}\right]_{12}^{24}=e^{-0,24}-e^{-0,48}\approx 0,1678\)
Le téléviseur a donc un peu moins de 17% de chances de tomber en panne entre la 1ere et la 2eme année.
Vérification à l'aide du tableur
En calculant la somme des fréquence sur les lignes entre 12 et 24 mois, on obtient la fréquence de panne constatée entre la 1ere et la seconde année.
On retrouve ainsi un résultat à peu près similaire.
En utilisant l'événement contraire, le téléviseur ne fonctionne plus au bout de deux ans signifie qu"il est tombé en panne sous garantie ou qu'il est tombé en panne entre la première et la deuxième année.
On a donc \(\mathbb P(T\geqslant 24)=1-\mathbb P(0\leqslant T \leqslant 12) - \mathbb P(12\leqslant T\leqslant 24) \approx 0,6188\)
Question
Calculer la probabilité que l'appareil fonctionne 5 ans sans une seule panne.
Solution
Pour que l'appareil fonctionne 5 ans sans une seule panne, il faut que la première panne arrive au delà de 60 mois. On cherche donc \(\mathbb P(T\geqslant 60)=1-\mathbb P(T< 60)=1-(1-e^{-1,2})=e^{-1,2}\approx 0,3012\)
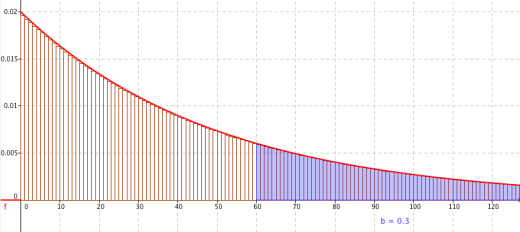
Il y a donc environ 30% de chances pour que le téléviseur survive à 5 ans.
Nous allons nous intéresser maintenant à la notion de vieillissement du téléviseur, en essayant d'en donner une définition mathématique.
Question
Sachant que le téléviseur est en parfait état de fonctionnement à la fin de la période de garantie, calculer la probabilité qu'il fonctionne encore un an de plus.
Comparer ce résultat à la probabilité fonctionne un an. Conclure.
Indice
Se rappeler du chapitre sur les probabilités conditionnelles !
Solution
Nous devons calculer\( \mathbb P_{(T\geqslant 12)}(T\geqslant 24)=\dfrac{\mathbb P(T\geqslant 24)}{\mathbb P(T\geqslant 12)}\approx \dfrac{0,6188}{0,7866}=0,7866\)
Remarque :
On constate que cette probabilité est exactement la même que celle de fonctionner après la première année !
En conclusion le fait que le téléviseur ait fonctionné correctement pendant un an n'a pas du tout affecté sa capacité à fonctionner sans panne un an de plus.
Question
On suppose que le téléviseur a 5 ans mais fonctionne encore. A t-il moins de chances de fonctionner encore un an de plus que lorsqu'il était neuf ? Vérifier cela par le calcul.
Qu'en déduit t-on sur le vieillissement du téléviseur ?
Solution
Nous devons calculer\( \mathbb P_{(T\geqslant 60)}(T\geqslant 72)=\dfrac{\mathbb P(T\geqslant 72)}{\mathbb P(T\geqslant 60)}=\dfrac{e^{-1,44}}{e^{-1,2}}\approx 0,7866\)
La probabilité que le téléviseur fonctionne encore une année est toujours de 0,7866. C'est donc autant de chances que de passer la période de garantie. On en conclut que le téléviseur n'a pas vieilli !