Loi exponentielle
Remarque :
Les lois exponentielles modélisent les processus qui ignorent le vieillissement comme par exemple la durée de vie de certains appareils électroniques, la durée de vie de certains éléments radioactifs ...
Définition : Propriété et Définition de la loi exponentielle
Soit \(\lambda\) un réel strictement positif. La fonction f définie sur \(\mathbb R^+\) par :
\(f~:~x\longmapsto \lambda e^{-\lambda x}\)
est une densité de probabilité sur \(\mathbb R^+\).
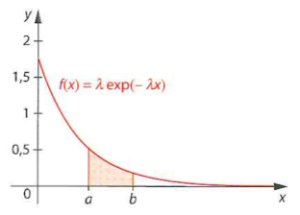
La loi de probabilité \(\mathbb P\) associée à cette fonction densité est appelée loi exponentielle de paramètre \(\lambda\). On la note \(\mathcal E(\lambda)\).
Si \(T\hookrightarrow \mathcal E(\lambda)\) et si a et b sont deux réels tels que\( 0\leqslant a<b\), on a :
\(\mathbb P(a\leqslant T\leqslant b)=\int_a^b \lambda e^{-\lambda x}~dt=\left[-e^{-\lambda t}\right]_a^b=e^{-\lambda a}-e^{-\lambda b}\)
Complément : Démonstration
La fonction \(f\) est continue et positive sur \(\mathbb R^+\).
De plus \(\lim\limits_{x\to +\infty} \int_0^x f(t)~dt=\lim\limits_{x\to +\infty} \left[-e^{-\lambda t}\right]_0^x = (\lim\limits_{x\to +\infty} 1-e^{-\lambda x} )=1-0=1\)
La fonction \(f\) est donc une fonction densité sur \(\mathbb R^+\).
Complément : Fonction de répartition
Si \(T\hookrightarrow \mathcal E(\lambda)\),
La fonction de répartition de \(T\) est la fonction \(F\) définie sur \(\mathbb R^+\) par \(F(x)=\mathbb P(T\leqslant x)\) soit
\(F~:~x\longmapsto 1-e^{-\lambda x}\)
En effet, on a bien \(F'(x)=f(x)\)
De plus \(F(0)=0=\mathbb P(T\leqslant 0)\) car La variable aléatoire T prend ses valeurs dans \(\mathbb R^+\) donc les événements \((T=0)\) et \((T\leqslant 0)\) sont identiques. Or on sait que \(\mathbb P(T=0)=0\) pour une loi continue sur \([0 ;+\infty[\).