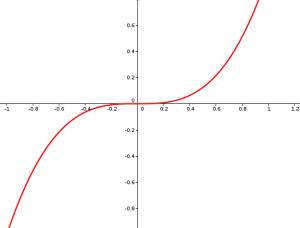
Point d'inflexion
La fonction cube est donc d'abord concave puis convexe d'après l'étude faite précédemment. Le changement de comportement de la fonction cube se passe en 0. Elle présente donc en 0 un point très particulier. La courbe ci-contre nous le montre en détail. La fonction ne change pas de sens de variation, néanmoins, la courbe s'infléchit en ce point particulier. En langage politicien, on pourrait parler de hausse de la baisse tendentielle !
En ce point très particulier, on ne peut pas dire que la courbe est au dessus ou en dessous de sa tangente, puisque justement elle change de comportement. La courbe \(\mathcal C\) traverse sa tangente \(\mathcal {T}_a\) (ici l'axe des abscisses) en ce point.
Définition : Point d'inflexion
On dit qu'un point A appartenant à \(\mathcal Cf\) est un point d'inflexion lorsque \(\mathcal Cf\) traverse sa tangente au point A.
Complément :
Par conséquent, en un point d'inflexion, la fonction passe de convexe à concave ou de concave à convexe.
La manière de déterminer ces points d'inflexion découle directement des propriétés précédentes :
Fondamental : Déterminer un point d'inflexion
Pour la courbe représentative d'une fonction deux fois dérivable sur un intervalle, le point d'abscisse, a est un point d'inflexion si et seulement si la dérivée seconde de cette fonction s'annule en a, en changeant de signe.
Exemple :
Pour la fonction cube étudiée plus haut, la dérivée seconde est \(x\longmapsto 6x\) qui s'annule bien en \(x=0\) mais surtout qui passe de négatif à positif en ce point. Le point \(O(0 ;0)\) est donc un point d'inflexion de la courbe représentative de la fonction cube.