Étude de la convexité d'une fonction
Question
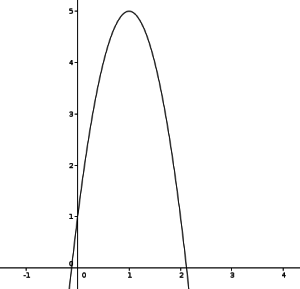
Étudier la convexité de la fonction \(f :x\longmapsto -4x^2+8x+1\)
Indice
On pourra étudier les variations de sa fonction dérivée
Solution
La dérivée de cette fonction du second degré est la fonction affine \(f' :x\longmapsto -8x+8\). Le coefficient directeur de cette fonction affine est négatif (-8) donc la fonction dérivée \(f'\) est décroissante sur \(\mathbb R\)
On en conclut que la fonction \(f\) est concave sur \(\mathbb R\), ce que confirme l'examen de sa courbe représentative.
Question
En généralisant l'étude précédente, que peut-on dire de la convexité des fonctions polynômes du second degré ?
Indice
Étudier la convexité de \(f :x\longmapsto ax^2+bx+c\) en fonction des coefficients a,b,c ou de l'un d'entre eux...
Solution
Soit \(f :x\longmapsto ax^2+bx+c\). On a f'(x)=2ax+b. Les variations de \(f'\) dépendent du signe de a:
Si \(a>0, f'\) est croissante donc \(f\) est convexe
Si \(a<0, f'\) est décroissante donc \(f\) est concave
On retrouve sans surprise la distinction entre les deux familles de polynômes du second degré en fonction du signe du coefficient dominant.