Introduction
Les notions de convexité et concavité vous sont déjà connues dans le cadre de la vie quotidienne. Les miroirs déformants dans les foires sont une illustration ludique de ces notions. Les lentilles optiques (loupes, lunettes ...) que nous utilisons en sont une application importante.
Nous allons voir dans ce chapitre l'application de ces notions dans le monde des fonctions. Cela a une utilité très importante dans le domaine de l'optimisation. Savoir si l'évolution d'un phénomène est convexe ou concave nous donne des informations très utiles pour mieux le connaître et prendre les bonnes décisions.
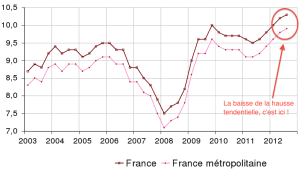
La notion d'inflexion que nous étudierons est également très commune. Une illustration anecdotique est son utilisation dans le domaine politique pour minimiser l'importance de la hausse du nombre de chômeurs.
Dans la vidéo ci-dessus, on note l'invention d'un nouveau concept : la baisse tendancielle de la hausse, qui mathématiquement pourrait se traduire par une inflexion. Nous étudierons cette notion plus en détail et nous verrons le lien entre inflexion et variation de la fonction dérivée.