La dérivée seconde
Exemple :
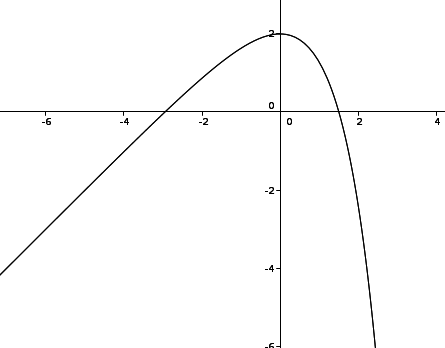
Supposons que l'on souhaite étudier la convexité de \(f :x\longmapsto 3+x-e^x\), on cherche alors à connaître les variations de \(f' :x\longmapsto1-e^x\)
Pour connaître les variations de cette fonction \(f'\), une méthode consiste à calculer ... sa dérivée et à étudier son signe !
La dérivée de \(f\)' est \(f''=-e^x\) dont le signe est toujours négatif. On en déduit donc que \(f'\) est toujours décroissante et par conséquent que \(f\) est concave sur \(\mathbb R\)
La démarche utilisée ci-dessus est assez classique et se résume au moyen de la méthode suivante :
Méthode :
Soit \(f\) une fonction deux fois dérivable sur un intervalle I
\(f\) est convexe si et seulement si pour tout \(x\in I, f''(x)\geqslant 0\)
\(f\) est concave si et seulement si pour tout \(x\in I, f''(x)\leqslant 0\)