Recherche d'un point d'inflexion
On considère la fonction définie sur \(\mathbb R\) par \(f :x\longmapsto x^3-6x^2+5x+10\)
Question
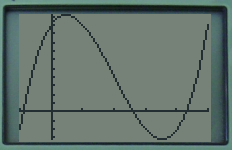
Tracer la courbe sur votre calculatrice et conjecturer graphiquement l'existence de points d'inflexions éventuels
Indice
Un tracé pour \(x\in[-1 ;5]\) devrait donner des informations pertinentes.
Solution
Sur la courbe ci-contre, on constate que la courbe est d'abord concave puis convexe. On devine donc l'existence d'un point d'inflexion qui sur le graphique semble se situer autour de \(x=2\)
Question
Question
Confirmer la conjecture faite à la première question
Solution
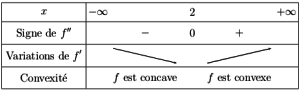
Le tableau ci-dessus montre que la dérivée seconde s'annule et change de signe en \(x=2\). Cela met en évidence un point d'inflexion au point d'abscisse 2 sur la courbe \(\mathcal Cf\) . Cela confirme la lecture faite sur la courbe.