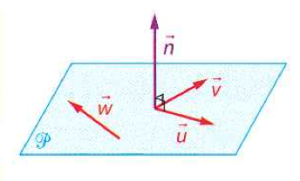
Vecteur normal à un plan
Définition : Vecteur normal à un plan
On appelle vecteur normal
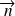à un plan un vecteur non nul orthogonal à tout vecteur de ce plan.
Remarque :
 | Il suffit que ce vecteur normal soit orthogonal à deux vecteurs non colinéaires du plan. |
En effet si
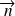est orthogonal à
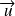et
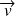, deux vecteurs non colinéaires du plan
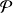, alors
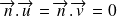
Soit un vecteur quelconque du plan
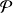. Celui-ci peut se décomposer comme combinaison de
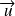et
:
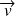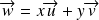où
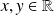
Et donc
.
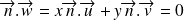Cette propriété va nous permettre de démontrer une propriété déjà rencontrée dans le chapitre sur l'espace sur l'orthogonalité droite-plan. Cette démonstration fera l'objet d'une ROC.
