ROC : Droite orthogonale à un plan
On a vu dans le chapitre sur l'espace qu'une droite est orthogonale à toute droite d'un plan si et seulement si elle est orthogonale à deux droites sécantes de ce plan.
Question
Supposons qu'une droite
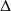soit orthogonale à deux droites
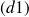et
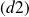d'un plan
.
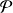Démontrer que
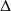est orthogonale à toute droite
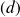incluse dans
.
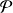On note
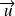un vecteur directeur de
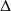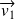et
et
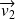des vecteurs directeurs de
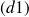et
.
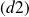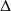est orthogonale aux deux droites
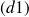et
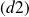donc le vecteur
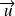est orthogonal aux vecteurs
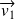et
.
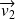Puisque
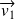et
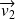dirigent
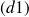et
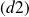, deux droites du plan
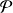, alors le vecteur
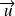est orthogonal à deux vecteurs
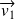et
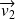du plan
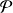. C'est donc
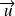est un vecteur normal du plan
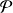d'après la propriété précédente.
On en déduit que le vecteur
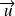est orthogonal à tout vecteur du plan
.
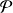Si
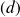est une droite incluse dans
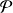dirigée par
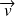, alors
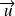et
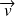sont orthogonaux.
Donc les droites
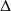et
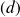sont orthogonales. CQFD.
