Intersection de deux plans
Dans un repère orthonormé, on considère les plans
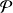et
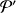d'équations respectives
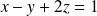et
.
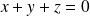Question
Montrer que les deux plans sont sécants et déterminer la nature et un système d'équations paramétriques de l'intersection.
On commencera par montrer que les deux plans ne sont pas parallèles.
Position relative des deux plans
Les plans ont pour vecteurs normaux les vecteurs
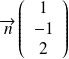et
.
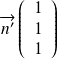Ces deux vecteurs ne sont pas colinéaires (on ne peut pas de coefficient de proportionnalité entre les deux), donc les plans ne sont pas parallèles.
Ils sont donc sécants suivant une droite
.
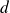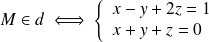
On peut écrire :
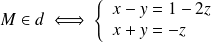
En additionnant et en soustrayant les deux équations membres à membres, on obtient :
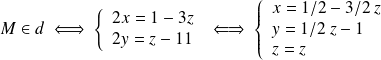
En posant t=z, obtient comme système d'équations paramétriques :
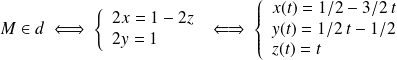ce qui est une représentation paramétrique d'une droite de vecteur directeur
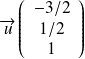et passant par le pointr de coordonnées (1/2 ;-1/2 ;0).
