Courbe représentative
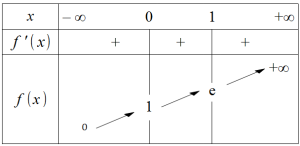
Tableau de variation de la fonction exp
Équation de la tangente en 0 à exp
On se rappelle de la formule permettant de calculer l'équation de la tangente à une fonction en un point.
Par conséquent, la tangente \(T_0\) en 0 à la fonction exp est \(y=e^0(x-0)+1\) donc \(y=x+1\).
De même, l'équation de la tangente \(T_1\) en 1 à la fonction exp est \(y=e^1(x-1)+e\) donc \(y=ex\) (à ne pas confondre avec \(e^x\) ! )
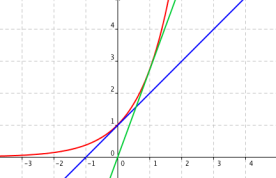
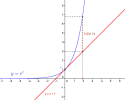
Fondamental : Position de la courbe de la fonction exponentielle par rapport à sa tangente au point d'abscisse 0.
La courbe de la fonction exponentielle est au dessus de la tangente au point d'abscisse 0. Le seul point de contact est le point de coordonnées (0 ;1).
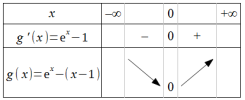
La fonction \(g\) définie sur \(\mathbb{R}\) par \(g(x)=e^x-(x-1)\) est toujours positive :
Il suffit de l'étudier pour s'en convaincre :
\(g\) est dérivable sur \(\mathbb{R}\) et pour tout \(x \in \mathbb{R}\), \(g'(x)=e^x-1\).
Pour connaître le signe de \(e^x-1\), résolvons l'inéquation \(e^-1>0\) :
\(e^x-1\ge0 \Leftrightarrow e^x\ge1\Leftrightarrow e^x\ge e^0 \Leftrightarrow x\ge 0\).
Exemple :
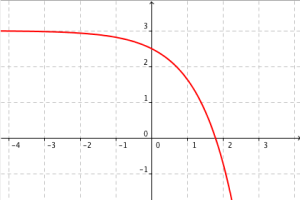
La fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=3-0,5e^x\) est dérivable sur \(\mathbb{R}\) et \(f'(x)=-0,5e^x\).
Comme pour tout réel \(x\), \(e^x\) est strictement positif, on en déduit que \(f'(x)\) est strictement négative sur \(\mathbb{R}\) donc \(f\) est strictement décroissante sur \(\mathbb{R}\).