Limite finie
Exemple :
Soit \((u_n)\) la suite définie par \(u_n=5\times0,2^n\).
Tous les termes de cette suite sont le produit de nombres strictement positifs et sont donc strictement positifs.
De plus l'étude des variations des suites géométriques nous apprend que comme la raison 0,2 est comprise strictement entre 0 et 1, la suite \((u_n)\) est strictement décroissante.
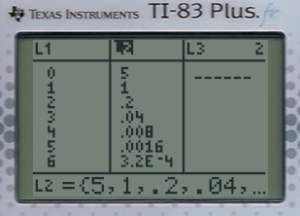
L'examen des premières valeurs de la suite à l'aide de la calculatrice montre que les valeurs tendent à se rapprocher de 0
Le graphe de la suite nous conforte dans l'idée que les valeurs se rapprochent très vite de 0.
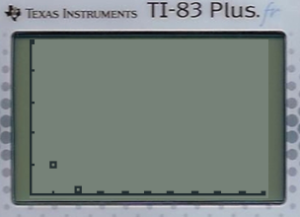
En réalité, on peut choisir un seuil aussi petit que l'on souhaite (par exemple un millionième (\(10^{-6}\))), on trouvera toujours un rang à partir duquel les valeurs de la suite passeront sous ce seuil.
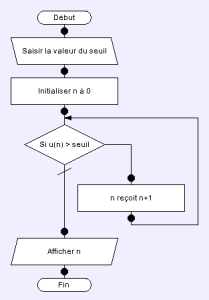
Le programme Python ci-dessous peut nous en convaincre. Il exploite une boucle tant que comme l'illustre l'algorithme correspondant ci contre.
seuil=input("Saisir la valeur du seuil ")n=0
while 5*0.2**n > seuil:
n=n+1
print "pour n=",n," on a un=",5*0.2**n
>>>
Saisir la valeur du seuil 0.000001
pour n= 10 on a un= 5.12e-07
Ainsi le seuil de un millionième est dépassé au delà du 10ème rang.
Le même programme implémenté en langage Casio serait :
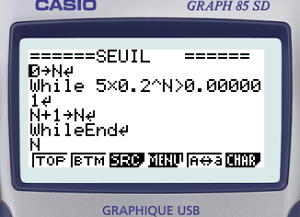
Définition :
Lorsque les termes d'une suite positive peuvent être rendus aussi proche de 0 que l'on veut, au delà d'un certain rang, on dit que cette suite tend vers 0 ou qu'elle converge vers 0.
On note alors :
\(\lim\limits_{n \to +\infty} u_n=0\)
Exemple :
Soit \((v_n)\) la suite définie par \(u_n=5\times(-0,3)^n\).
Avec la calculatrice, il semble aussi que \(\lim\limits_{n \to +\infty} v_n=0\) :