Limite d'une somme
Reprenons l'exemple de l'exercice du paragraphe précédent avec la somme des inverses des puissances de 2.
\(S_n=1+\dfrac{1}{2}+\dfrac{1}{2^2}+ ... + \dfrac{1}{2^n}\)
Question
Étudier le comportement de cette somme lorsque n tend vers l'infini
Indice
On pourra calculer explicitement \(S_n\) en fonction de \(n\)
Solution
\(S_n\) est la somme des termes d'une suite géométrique de premier terme 1 et de raison \(\dfrac{1}{2}\)
La formule du cours s'applique et donne \(S_n=1\times\dfrac{1-\left(\dfrac{1}{2}\right)^{n+1}}{1-\dfrac{1}{2}}\)
Or la division par 1-0,5 revient à une multiplication par 2.
Donc \(S_n=2\left(1-\left(\dfrac{1}{2}\right)^{n+1}\right)\)
Or on sait que quand n tend vers l'infini, \(\left(\dfrac{1}{2}\right)^{n+1}\) tend vers 0 car \(0<\dfrac{1}{2}<1\)
Par conséquent \(1-\left(\dfrac{1}{2}\right)^{n+1}\) tend vers 1 puisque le second terme devient nul
et donc \(\lim\limits_{n \to +\infty} S_n=2\)
Ce qui démontre le résultat conjecturé sur l'ordinateur au paragraphe précédent.
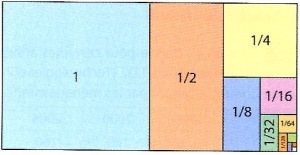
Graphiquement, on peut interpréter cette somme finie d'une infinité de termes en considérant que les termes en \(\dfrac{1}{2^n}\) sont en fait les aires de rectangles dont on divise une longueur du coté par 2 à chaque étape. L'ensemble de tous les rectangles peut tenir dans un rectangle dont l'aire totale est la limite de la somme \(S_n\) à savoir 2.