À partir d'un carré de côté 1, on construit étape par étape d'autres carrés pour obtenir les figures suivantes :

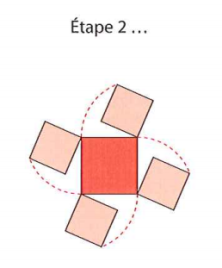
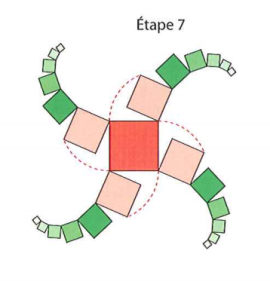
Question
Peut-on trouver une étape à partir de laquelle l'aire de la figure dépasse 5 ?
Indice
Définir des suites donnant le côté de chaque type de carré obtenus à chaque étape, l'aire de chacun de ces carrés, et la somme totale.
Solution
Soit \((c_n)_{n\ge1}\)la suite donnant les côtés successifs des côtés des nouveaux carrés construits à chaque étape :
\(c_1=1\)
\(c_2=c_1\times\dfrac{1}{\sqrt{2}}\)
En effet, la diagonale des nouveaux carrés de l'étape 2 est égale au côté du carré initial, donc il faut diviser \(c_1\) par \(\sqrt{2}\).
De même :
\(c_3=c_2\times \dfrac{1}{\sqrt{2}}=\dfrac{1}{2}\)
...
\(c_{n+1}=c_n\times\dfrac{1}{\sqrt{2}}=c_n\times\dfrac{\sqrt{2}}{2}\)
La suite \((c_n)_{n\ge1}\) est une suite géométrique de 1er terme =1 et de raison \(\dfrac{\sqrt{2}}{2}\), donc, \(c_n=\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\).
L'aire de chaque carré est donc \(a_n=(c_n)²=\left({\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}}\right)^2=\left({\left(\dfrac{\sqrt{2}}{2}\right)^{2}}\right)^{n-1}\), donc :
\(a_n=\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{2^{n-1}}\)
L'aire totale à l'étape 2 est :
\(1+4a_2=1+4\times\dfrac{1}{2}\)
L'aire totale à l'étape 3 est :
\(1+4a_2+4a_3=1+4\times\dfrac{1}{2}+4\times\dfrac{1}{2²}\)
L'aire totale à l'étape n (pour ) est égale à :
\(1+4a_2+4a_3+...+4a_n=1+4\times\dfrac{1}{2}+4\times\dfrac{1}{2²}+4\times\dfrac{1}{2^3}+...+4\times\dfrac{1}{2^{n-1}}\)
\(=1+4\times\left(\dfrac{1}{2}+\dfrac{1}{2²}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{n-1}}\right)\)
\(=1+4\times \dfrac{1}{2}\left(1+\dfrac{1}{2}+\dfrac{1}{2²}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{n-2}}\right)\)
\(=1+2\times\left(\dfrac{1-\dfrac{1}{2^{n-1}}}{1-\dfrac{1}{2}}\right)\)
\(=1+2\times2\times\left(1-\dfrac{1}{2^{n-1}}\right)\)
\(1+4\times\left(1-\dfrac{1}{2^{n-1}}\right)\)
\(=1+4-4\times\dfrac{1}{2^{n-1}}\)
\(=5-\dfrac{1}{2^{n-3}}\)
Donc l'aire l'aire totale de la figure est toujours inférieure à 5.
D'autre part, on peut constater que la limite quand n tend vers \(+\infty\) de l'aire de la figure est 5, car \(\dfrac{1}{2^{n-3}}\)tend vers 0 quand n tend vers \(+\infty\) (on reverra cette notion en terminale).