Rappel et Définition
Rappel : La fonction exponentielle
La fonction exponentielle est continue et strictement croissante sur \(\mathbb{R}\) et à valeurs dans \(\mathbb{R}^+\), c'est à dire que les images de tous les nombres réels sont des nombres réels positifs.
Pour tout réel \(a\in]0 ;+\infty[\), l'équation \(e^x=a\) admet une unique solution dans \(\mathbb{R}\) (c'est une conséquence du théorème des valeurs intermédiaires).
Définition : Logarithme néperien
On appelle logarithme népérien d'un réel strictement positif \(a\), l'unique solution de l'équation \(e^x=a\). On le note \(\ln a\).
La fonction \(\ln\) qui à \(x\) associe \(\ln x\) est définie sur l'intervalle \(]0 ;+\infty[\).
Exemple :
L'équation \(e^x=5\) admet une unique solution. On le sait grâce au Théorème des Valeurs Intermédiaires car :
\(x\longmapsto e^x\) est continue sur \(\mathbb{R}\)
\(x\longmapsto e^x\) est strictement croissante sur \(\mathbb{R}\)
\(4.953\approx e^{1.6} < 5 < e^{1.61}\approx 5,002\)
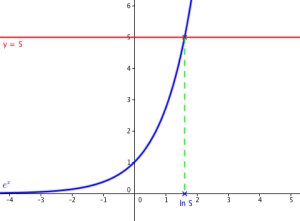
Le nombre unique tel que \(e^x=5\) est \(\ln 5\). La calculatrice nous en donne une valeur approchée : \(x\approx 1.6094\)
Attention : Pas de logarithme de nombres négatifs !
Il apparaît clairement sur la figure que si \(a\le 0\), la droite rouge d'équation \(y=a\) ne rencontre pas la courbe bleue de l'exponentielle. Il n'y a donc pas de point d'intersection donc pas de logarithme pour les nombres négatifs.
La fonction ln est définie sur l'intervalle \(]0 ;+\infty[\).