Premières propriétés
Fondamental : Conséquences de la définition du logarithme
On obtient de la définition précédente que :
si \(x>0\), \(y=\ln x\) si et seulement si \(x=e^y\)
\(\ln 1=0\) ; \(\ln e = 1\) ; \(\ln \dfrac{1}{e}=-1\)
Pour tout nombre réel \(x\), on a \(\ln~e^x=x\)
Pour tout nombre réel positif \(x\), on a \(e^{\ln x}=x\)
Complément : Démontration
Découle directement de la définition
\(e^0=1\) donc \(0=\ln 1\)
\(e^1=e\) donc \(\ln e=1\)
\(e^{-1}=\dfrac{1}{e}\) donc \(\ln \dfrac{1}{e}=-1\)
Si on pose \(y=e^x\), alors \(x=\ln y=\ln~ e^x\)
Si on pose \(y=\ln x\) pour \(x\) positif, alors \(x=e^y=e^{\ln x}\)
Exemple :
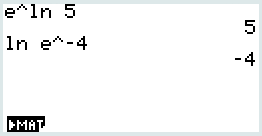
\(e^{\ln 5}=5\)
\(\ln e^{-4}=-4\)
mais attention, \(e^{ln(-4)}\ne-4\) car \(ln(-4)\) n'existe pas !