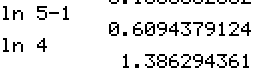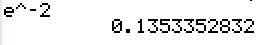Résoudre des équations simples
Résoudre dans \(\mathbb{R}\) les équations suivantes :
Question
Question
\(e^{x+1}=5\)
Indice
Pour tout \(x\), \(x=e^{\ln x}\)
Solution
Méthode :
\(e^{x+1}=5\) équivaut à \(e^{x+1}=e^{\ln 5}\)
Or la fonction exponentielle est strictement croissante sur \(\mathbb{R}\) donc l'équation se ramène à une équation sans exponentielle :
\(x+1=\ln 5\). La solution est donc \(x=\ln 5-1\).
Attention :
On ne confondra bien sûr pas \(\ln 5-1\) et \(\ln 4\) ! !