Conséquences immédiates
De la relation fonctionnelle, nous déduisons aisément plusieurs propriétés calculatoires très utilisées.
Fondamental :
Pour tous réels x et y strictement positifs, on a
\(\ln \dfrac{1}{x}=-\ln x\)
\(\ln \dfrac{x}{y}=\ln x - \ln y\)
\(\ln \sqrt{x}=\dfrac{1}{2}\ln x\)
\(\ln x^n=n\ln x\) pour tout entier relatif n
Complément : Démonstration
\(\ln \dfrac{1}{x}+\ln x=\ln\left(\dfrac{1}{x}\times x\right)=\ln 1=0\)
\(\ln \dfrac{x}{y}=\ln\left( x\times \dfrac{1}{y}\right)=\ln x+\ln\dfrac{1}{y}=\ln x-\ln y\)
\(2\ln\sqrt{x}=\ln \sqrt{x}+\ln \sqrt{x}=\ln\left(\sqrt{x}\times \sqrt{x}\right)=\ln x\)
\(e^{n\ln x}=\left(e^{\ln x}\right)^n=x^n=e^{\ln x^n}\)
Exemple :

\(\ln \dfrac{3}{4}=\ln 3 -\ln 4\)
\(\ln\sqrt 5=\dfrac{1}{2}\ln 5\)
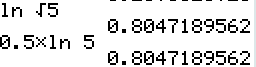
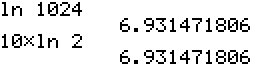
\(\ln 1024=\ln (2^{10})=10\ln2\)