Marche aléatoire (TP3 p382)
On étudie le mouvement aléatoire d'une puce. Cet puce se déplace sur trois cases notées A, B et C. À l'instant 0, la puce est en A.
pour tout entier naturel n:
si à l'instant n la puce est en A, alors à l'instant n+1, la puce est
soit en B avec une probabilité égale à \(\frac{1}{3}\)
soit en C avec une probabilité égale à \(\frac{2}{3}\)
si à l'instant n la puce est en B, alors à l'instant n+1, la puce est
soit en A avec une probabilité égale à \(\frac{1}{2}\)
soit en C avec une probabilité égale à \(\frac{1}{2}\)
si à l'instant n la puce est en C, alors elle y reste.
On note \(A_n\) (respectivement \(B_n\) et \(C_n\)) l'événement « à l'instant n la puce est en A »
(respectivement B et C)
On note \(a_n\) (respectivement \(b_n\) et \(c_n\)) la probabilité de l'événement \(A_n\) (respectivement \(B_n\) et \(C_n\))
On a donc \(a_0=1, b_0=c_0=0\)
Partie A : Algorithmique
On code la case A par 0, la case B par 1 et C par 2. On nomme
pos la variable qui contient la position de la puce à un instant donné, c'est à dire la valeur 0, 1 ou 2.
tirage la variable qui contiendra un tirage aléatoire d'un nombre entre 0 et 1
Question
Recopier et compléter les ? ? ? dans l'algorithme ci-dessous pour simuler le passage de l'instant donné à l'instant suivant.
pos contient la position de la puce
tirage prend une valeur aléatoire entre 0 et 1
Si pos=0,
... Si tirage < 1/3,
... ... a prend la valeur ? ? ?
... Sinon,
... ... a prend la valeur ? ? ?
... Fin Si
Sinon Si pos=1,
... Si tirage<1/2,
... ... a prend la valeur ? ? ?
... Sinon,
... ... a prend la valeur ? ? ?
... Fin Si
Sinon si pos=2
... a prend la valeur ? ? ?
Fin Si
pos prend la valeur ? ? ?
Solution
pos contient la position de la puce
tirage prend une valeur aléatoire entre 0 et 1
Si pos=0,
... Si tirage < 1/3,
... ... a prend la valeur 1
... Sinon,
... ... a prend la valeur 2
... Fin Si
Sinon Si pos=1,
... Si tirage<1/2,
... ... a prend la valeur 0
... Sinon,
... ... a prend la valeur 2
... Fin Si
Sinon si pos=2
... a prend la valeur 2
Fin Si
pos prend la valeur a
Question
Compléter l'algorithme pour simuler une marche aléatoire à n étapes, n étant donné par l'utilisateur au départ
Solution
n prend une valeur donnée par l'utilisateur
pos prend la valeur 0
Pour i allant de 1 à n,
... tirage prend une valeur aléatoire entre 0 et 1
... Si pos=0,
... ... Si tirage < 1/3,
... ... ... a prend la valeur 1
... ... Sinon,
... ... ... a prend la valeur 2
... ... Fin Si
... Sinon Si pos=1,
... ... Si tirage<1/2,
... ... ... a prend la valeur 0
... ... Sinon,
... ... ... a prend la valeur 2
... ... Fin Si
... Sinon si pos=2
... ... a prend la valeur 2
... Fin Si
... pos prend la valeur a
Fin Pour
Afficher pos
Question
Compléter à nouveau l'algorithme de manière à simuler 1000 marches de n étapes et afficher les fréquences d'arrivée en A, B et C au cours de ces 1000 marches
Solution
n prend une valeur donnée par l'utilisateur
A prend la valeur 0
B prend la valeur 0
C prend la valeur 0
Pour m allant de 1 à 1000,
... pos prend la valeur 0
... Pour i allant de 1 à n,
... ... tirage prend une valeur aléatoire entre 0 et 1
... ... Si pos=0,
... ... ... Si tirage < 1/3,
... ... ... ... a prend la valeur 1
... ... ... Sinon,
... ... ... ... a prend la valeur 2
... ... ... Fin Si
... ... Sinon Si pos=1,
... ... ... Si tirage<1/2,
... ... ... ... a prend la valeur 0
... ... ... Sinon,
... ... ... ... a prend la valeur 2
... ... ... Fin Si
... ... Sinon si pos=2
... ... ... a prend la valeur 2
... ... Fin Si
... ... pos prend la valeur a
... Fin Pour i
... Si pos=0, Alors A prend la valeur A+1
... Sinon Si pos=1, Alors B prend la valeur B+1
... Sinon Si pos=2, Alors C prend la valeur C+1
Fin Pour m
Afficher A/1000
Afficher B/1000
Afficher C/1000
Question
Programmer cet algorithme dans le langage de votre choix.
On prendra n=4.
Quelles fréquences obtenez-vous ?
Solution
Voici le listing du programme en python
from random import random
n=4
A,B,C=0,0,0
for m in range(1000):
... pos=0
... for i in range(n):
... ... tirage=random()
... ... if pos==0:
... ... ... if tirage<1/3:
... ... ... ... a=1
... ... ... else:
... ... ... ... a=2
... ... elif pos==1:
... ... ... if tirage <1/2:
... ... ... ... a=0
... ... ... else:
... ... ... ... a=2
... ... elif pos==2:
... ... ... ... a=2
... ... pos=a
... if pos==0:
... ... A=A+1
... elif pos==1:
... ... B=B+1
... elif pos==2:
... ... C=C+1
print (A/1000)
print (B/1000)
print (C/1000)
On obtient une fréquence
pour A de 0,033
pour B de 0
pour C de 0,967
Partie B : Théorie
Nous allons à présent calculer les probabilités théoriques et confronter ces résultats avec la simulation réalisée ci-dessus.
Question
Illustrer par un arbre pondéré les positions possibles de la puce aux instants n et \(n+1\).
Calculer ensuite \(a_k, b_k\) et \(c_k\) pour \(1\leqslant k\leqslant 3\).
Solution
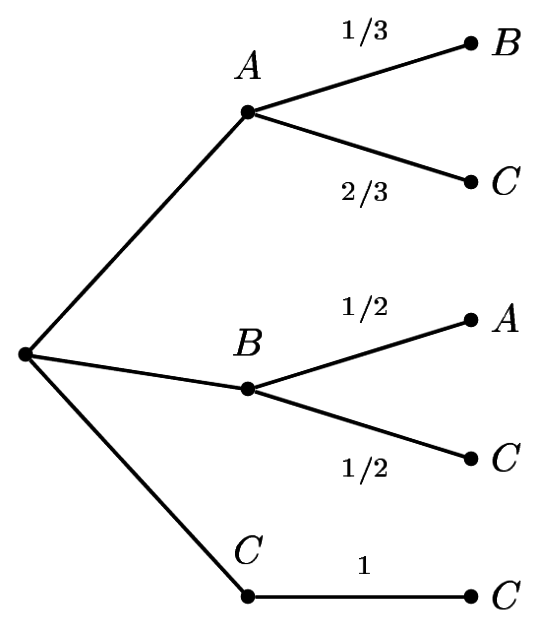
Pour k =1, on vient de A. Donc :
\(a_1=0\)
\(b_1=\frac{1}{3}\)
\(c_1=\frac{2}{3}\)
On vérifie que \(a_1+b_1+c_1=1\)
Pour k=2, on vient de B ou de C. On a donc :
\(a_2=\frac{1}{3}\times\frac{1}{2}+0=\frac{1}{6}\)
\(b_2=0\)
\(c_2=\frac{1}{3}\times \frac{1}{2}+\frac{2}{3}\times 1=\frac{5}{6}\)
On vérifie que \(a_2+b_2+c_2=1\)
Pour k=3, on vient de A ou de C. On a donc
\(a_2=0\)
\(b_2=\frac{1}{3}\times\frac{1}{6}=\frac{1}{18}\)
\(c_2=\frac{2}{3}\times \frac{1}{6}+\frac{5}{6}\times 1=\frac{17}{18}\)
On vérifie que \(a_3+b_3+c_3=1\)
Question
Montrer que pour tout entier naturel n, \(a_{n+2}=\frac{1}{6}a_n\)
Solution
Si la puce est sur la case A, au rang suivant elle sera sur B ou C. Deux rang plus tard, elle sera sur A ou C.
Pour qu'elle se retrouve sur A à nouveau deux étapes plus tard, il faut qu'elle aille sur B puis sur A. Il faut donc calculer le produit des probabilités soit \(\frac{1}{3}\times \frac{1}{2}\) soit \(\frac{1}{6}\) de la probabilité de départ.
Si la puce n'est pas en A, deux rangs plus tard, elle ne peut pas non plus être en A, donc la probabilité reste nulle.
Donc \(a_{n+2}=\frac{1}{6}a_n\).
Question
Montrer que pour tout entier naturel n, \(b_{n+2}=\frac{1}{6}b_n\).
Solution
On procède au même raisonnement que précédemment. Pour aller de B à B en deux étapes, elle devra nécessairement passer par A puis par B. Le premier chemin de B vers A a une probabilité de \(\frac{1}{2}\) et le second de A vers B de \(\frac{1}{3}\). Au final, la probabilité du chemin B->A->B est \(\frac{1}{6}\)
Question
Expliquer pourquoi pour tout entier naturel \(p\) :
\(a_{2p}=\left(\frac{1}{6}\right)^p\) et \(a_{2p+1}=0\)
\(b_{2p}=0\) et \(b_{2p+1}=\frac{1}{3}\left(\frac{1}{6}\right)^p\)
Solution
Si on exclut la case C qui laisse la puce sur place, la puce partant de A ne peut revenir vers A que tous les 2 tours. De même partant de B, elle ne peut revenir vers B que tous les deux tours.
La case de départ étant A, tous les tours impairs, on est sur que la puce n'est pas en A donc \(a_{2n+1}=0\)
On a vu que \(b_1=\frac{1}{3}\) et donc à tous les tours pairs, il est impossible que la puce soit en B. donc \(b_{2n}=0\)
Enfin, à chaque fois que p augmente de 1, donc tous les deux tours, la probabilité de la case A ou B est multipliée par \frac{1}{6} d'après la question précédente.
On en déduit donc les égalités demandées.
Question
Montrer que pour tout n, \(a_n+b_n+c_n=1\)
Solution
La puce se trouve sur A, sur B ou sur C, il n'y a pas d'autre possibilité. De plus, les événements \(A_n\), \(B_n\) et \(C_n\) sont disjoints donc la somme de leur probabilités vaut 1.
Question
Montrer que \(\lim\limits_{n \to +\infty} a_n=0\) et \(\lim\limits_{n \to +\infty} b_n=0\)
En déduire \(\lim\limits_{n \to +\infty} c_n\)
Solution
On sait que la limite d'une suite géométrique de raison \(\frac{1}{6}\) est nulle.
Donc \(\lim\limits_{n \to +\infty} a_{2n}=0\)
De plus \(\lim\limits_{n \to +\infty} a_{2n+1}=0\) car la suite \(a_{2n+1}\) est constamment égale à 0
On en déduit que la suite \((a_n)\) tend vers 0.
On procède de même pour la suite \((b_n)\)
On sait que \(a_n+b_n+c_n=1\) donc d'après les opérations sur les limites \(\lim\limits_{n \to +\infty} a_n+b_n+\lim\limits_{n \to +\infty} c_n=1\). Or la première limite est nulle car chacune des suites tend vers 0 donc \(\lim\limits_{n \to +\infty} c_n=1\)
Question
Cela est-il cohérent avec votre simulation réalisée en partie 1 ?
Solution
Oui, déjà pour n=4 on obtenait une fréquence pour B de 0, une pour A proche de 0 et pour C, proche de 1.