ROC : Indépendance et événement contraire
Si \(A\) et \(B\) sont deux événements indépendants, alors \(\bar{A}\) et \(B\) le sont aussi.
Question
ROC : Démontrer ce résultat
Solution
Méthode : **ROC** Démonstration
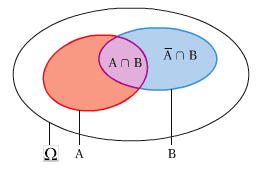
L'événement \(A\cap B\) et l'événement \(\bar{A}\cap B\) sont deux événements incompatibles.
La réunion de ces deux événements est l'événement B.
On peut alors écrire que \(P(B)=P(\bar A \cap B)+P(A \cap B)\)
Or A et B sont indépendants donc \(P(B)=P(A)\times P(B)+P(\bar A\cap B)\)
Donc \(P(\bar A\cap B)=P(B)-P(A)\times P(B)\).
En mettant \(P(B)\) en facteur : \(P(\bar A\cap B)=(1-P(A))P(B)\)
Or \(1-P(A)=P(\bar A)\) donc \(P(\bar A\cap B)= P(\bar A)\times P(B)\). CQFD