Utiliser les théorèmes de convergence monotone

On considère la suite \((u_n)\) définie par

  • \(u_0=\frac{3}{2}\)

  • \(u_{n+1}=u_n^2-2u_n+2\)

Question

Démontrer que pour tout \(n\in \mathbb N, 1\leqslant u_n\leqslant 2\)

Indice

On pourra utiliser un raisonnement par récurrence.

Indice

On pourra remarquer que \(u_{k+1}=(u_k-1)^2+1\)

Solution

Posons \(\mathcal P_n\) la propriété que \(1\leqslant u_n\leqslant 2\)

  1. Initialisation

    \(u_0=1,5\) donc compris entre 1 et 2. \(\mathcal P_0\) est vraie.

  2. Hérédité

    Supposons que pour un certain rang k, \(\mathcal P_k\) soit vraie

    \(u_{k+1}=u_k^2-2u_k+2\)

    \(u_{k+1}=(u_k-1)^2+1\). Or \(0\leqslant u_k-1\leqslant 1\), il en est donc de même pour \((u_k-1)^2\)

    Donc \(1\leqslant (u_k-1)^2+1\leqslant 2\)

    par conséquent \(1\leqslant u_{k+1}\leqslant 2\) ce qui prouve que \(\mathcal P_{k+1}\) est vraie.

  3. Conclusion

    Par récurrence, on en déduit que pour tout \(n\in \mathbb N, 1\leqslant u_n\leqslant 2\).

Question

Montrer que pour tout n, on a \(u_{n+1}-u_n=(u_n-2)(u_n-1)\).

Solution

En développant, on obtient que \((u_n-2)(u_n-1)=u_n^2-3u_n+2=u_{n+1}-u_n\).

Question

Démontrer que \((u_n)\) est décroissante.

Indice

Quel est le signe de \(u_{n+1}-u_n\) ?

Solution

La première question nous permet de dire que pour tout n :

  • \(u_n-1 \geqslant 0\)

  • \(u_n-2 \leqslant 0\)

La seconde question permet de remarquer que le signe de \(u_{n+1}-u_n\) est le même que celui du produit \((u_n-1)(u_n-2)\) donc négatif pour tout n.

On en déduit donc que \((u_n)\) est décroissante.

Question

La suite \((u_n)\) est-elle convergente ?

Solution

La suite \((u_n)\) est décroissante et minorée donc on peut affirmer grâce au théorème de convergence monotone que \((u_n)\) converge.

Question

Déterminer la limite de la suite \((u_n)\).

Indice

On pourra s'appuyer sur les théorèmes d'opération pour déterminer une équation vérifiée par la limite \(\ell\).

Solution

  • \(u_{n+1}\) tend vers \(\ell\)

  • \(u_n^2-2u_n+2\) tend vers \(\ell^2-2\ell+2\)

La limite \(\ell\) est donc une solution de l'équation \(\ell=\ell^2-2\ell+2\)

L'équation \(\ell^2-3\ell+2=0\) admet deux solutions : \(\ell=1\) et \(\ell=2\)

Or la solution \(\ell=2\) est à rejeter car \(u_0=\frac{3}{2}\) et \((u_n)\) est décroissante.

On en déduit donc que la limite de la suite \((u_n)\) est \(\lim\limits_{n\to\infty} u_n=1\)

Question

Interpréter géométriquement ce phénomène

Indice

Pour les suites définies par une récurrence du type \(u_{n+1}=f(u_n)\), il est souvent commode de tracer sur un même graphique la courbe \(y=f(x)\) et la droite \(y=x\)

Solution

Méthode

  1. On trace sur le même graphique la courbe \(\mathcal C_f : y=x^2-2x+2\) et la droite \(\Delta : y=x\)

  2. On place le point \(A(1,5 ;1,5)\) correspondant au départ de la suite (\(u_0=1,5\))

  3. Depuis ce point, on rejoint la courbe \(\mathcal C_f\) et on reporte l'ordonnée sur la droite \(\Delta\). On obtient un nouveau point dont les coordonnées matérialisent \(u_1\)

  4. On répète l'étape précédente autant de fois que nécessaire pour matérialiser les premiers termes de la suite.

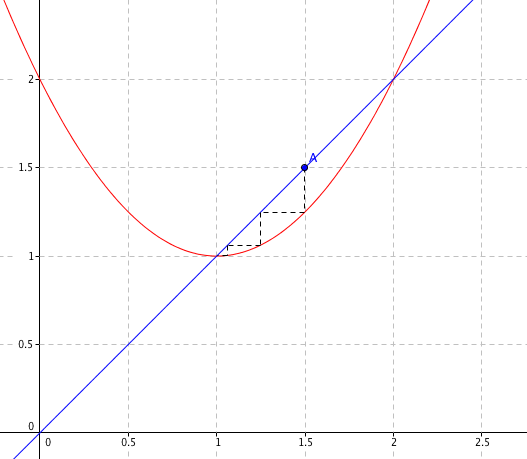
Complément

On s'aperçoit dans cette construction que la suite est décroissante puisque les points de \(\Delta\) se rapprochent de l'origine au fur à mesure de la construction

De plus on constate que la construction forme une sorte d'escargot qui se retrouve coincé au point où les courbes \(\mathcal C_f\) et \(\Delta\) se croisent. Ce point d'intersection des deux courbes est donc la limite de la suite.

On retrouve ainsi géométriquement que la limite de la suite \((u_n)\) est une des deux solutions de l'équation \(f(x)=x\) (ici \(x=1\))