Fonction exponentielle de base q avec q>0
Soit q un nombre strictement positif donné. La suite de terme général \(u_n=q^n\) pour tout entier naturel n est une suite géométrique de raison q.
La fonction exponentielle de base q est le prolongement de cette suite géométrique à l'ensemble des réels. Elle est définie sur \(\mathbb{R}\) par \(f(x)=q^x\) avec \(q>0\).
Exemple : Fonction exponentielle de base 1,21
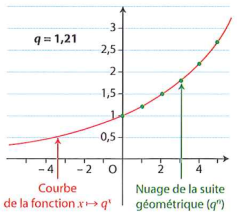
Prenons q=1,21. La fonction \(x\longmapsto1,21^x\) prolonge la suite géométrique \(1,21^n\) sur \(\mathbb{R}\).
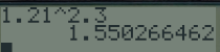
A l'aide de la calculatrice, on peut calculer les valeurs de cette fonction pour n'importe quel réel en utilisant la touche puissance (^) habituelle. Ainsi, \(1,21^{2,3}\approx 1,55\).
Complément : Cas particulier
La fonction exponentielle prolongeant la puissance que nous connaissons de longue date, on a toujours les égalités suivantes :
\(q^0=1\) donc la courbe représentant la fonction passe par le point de coordonnées (0 ; 1) quelque soit q (q>0)
\(q^1=q\) donc la courbe représentant la fonction passe par le point de coordonnées (1 ; q)
\(q^{-1}=\dfrac{1}{q}\)
Pour tout réel \(x\), \(1^x=1\)