Sens de variations
Rappel :
On se rappelle du sens de variation des suites géométriques.
On admettra que le sens de variation des fonctions exponentielles de base q avec q>0 est le même que celui de la suite géométrique associée. En d'autres termes :
Fondamental : Propriété admise : variation de la fonction exponentielle de base q avec q>0
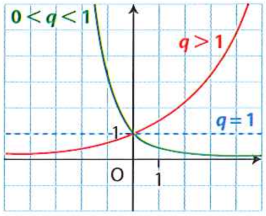
En continuité avec les suites numériques, on admet que :
si \(q>1\), la fonction \(x\longmapsto q^x\) est strictement croissante sur \(\mathbb{R}\)
si \(0<q<1\), la fonction \(x\longmapsto q^x\) est strictement décroissante sur \(\mathbb{R}\)
si \(q=1\) la fonction \(x\longmapsto 1^x=1\) est constante sur \(\mathbb{R}\)
Complément : Conséquences
Si \(q\neq1\) alors, pour tous nombres réels \(a\) et \(b\), \(q^a=q^b\) si et seulement si \(a=b\).
De plus :
Si \(q>1\), alors pour tous nombres réels \(a\) et \(b\), \(a<b\) si et seulement si \(q^a<q^b\) : exemple : \(1,21^{0.5}<1,21^{0,7}\).
et
Si \(q<1\), alors pour tous nombres réels \(a\) et \(b\), \(a<b\) si et seulement si \(q^a>q^b\) : exemple : \(0,8^{0.5}>0,8^{0,7}\).