Exemple et calcul
Exemple :
Un commercial négocie son salaire. A la base, celui-ci est de 1500€ net. Il négocie une augmentation de 12% par an mais ses frais de restauration s'élevant à 140€ par mois restent à sa charge.
On note \(u_n\) le salaire mensuel à l'année n. Identifier le type de suite auquel correspond \((u_n)\) puis calculer le salaire de cet employé après 4 années d'augmentation.
Nous avons \(u_0=1500\) qui correspond au salaire initial.
Ensuite, le salaire mensuel net d'une année est égal au salaire mensuel de l'année précédente augmenté de 12%, mais auquel on retranche 140€. Cela se traduit donc par l'égalité :
\(u_n=1,12\times u_{n-1}-140\) pour tout \(n\geq 1\)
Méthode : Calcul de u4 de proche en proche
On peut utiliser la formule de récurrence pour calculer \(u_4\). Il faut pour cela calculer les valeurs successives pour n=1, 2, 3 puis 4.
\(u_1=1,12\times 1500-140=1540\)
\(u_2=1,12\times 1540-140=1584,80\)
\(u_3=1,12\times 1584,80-140=1634,98\)
\(u_4=1,12\times 1634,98-140=1691,17\)
Son salaire net au bout de 4 années d'augmentation sera donc de 1691,17€.
Méthode : Calcul de u4 à l'aide du tableur
Méthode : Calcul de u4 à l'aide d'un programme
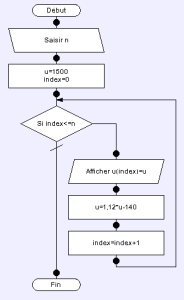
L'algorithme ci-contre demande à l'utilisateur de saisir la valeur de n pour laquelle il souhaite connaître \(u_n\). Le programme initialise la valeur de la suite à 1500 qui correspond à l'index 0 puis initie une boucle qui va calculer la valeur suivante de u en utilisant la formule de récurrence.
L'affichage des valeurs de \(u_n\) se fait au fur et à mesure pour connaître toutes les valeurs de la suite jusqu'au rang n. On pourrait aussi déporter cet affichage à la sortie de la boucle mais dans ce cas, seule la valeur \(u_n\) finale serait affichée.
n=input("Saisir la valeur de n ")u=1500
for index in range(n+1):
print "u(",index,")=",uu=1.12*u-140
Ci-dessus est donnée une implémentation Python de cet algorithme. On remarquera le n+1 passé à la commande range. En effet, range(k) renvoie la liste des k valeurs comprises entre 0 et k-1. Nous voulons que notre boucle inclue une valeur de l'index égale à n.
Et voici la sortie obtenue sur la console:
>>>
Saisir la valeur de n 4
u(0)= 1500
u(1)= 1540.0
u(2)= 1584.8
u(3)= 1634.976
u(4)= 1691.17312
On y retrouve la valeur de \(u_4\) cherchée.
A vous en exercice d'implémenter cet algorithme sur votre propre calculatrice en mode programmation.