On considère la relation de récurrence \(u_{n+1}=0,5u_n+3\)
On se propose d'étudier graphiquement le comportement de la suite \((u_n)\) pour le cas où \(u_0=2\) et \(u_0=6\).
Question
Représenter dans un repère les droites D d'équation \(y=x\) et Δ d'équation \(y=0,5x+3\).
Représenter ensuite sur ce même graphique :
en vert les termes de la suite \((u_n)\) pour \(\)\(u_0=2\)
en rouge les termes de la suite \((u_n)\) pour \(u_0=11\)
Solution
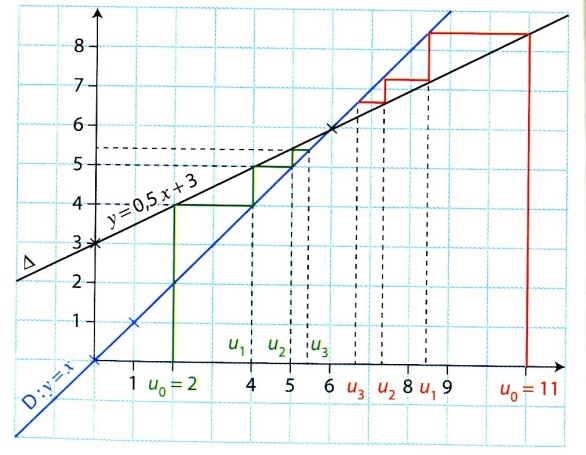
On a représenté sur le graphique ci-dessous la suite pour deux valeurs différentes de \(u_0\) : \(u_0=2\) en vert et \(u_0=11\) en rouge.
Question
Que peut-on dire du sens de variation de la suite \((u_n)\) pour chacun des deux cas étudiés ?
Dans chacun de ces deux cas, que peut-on dire de la convergence de la suite \((u_n)\) ?
Solution
L'examen du graphique permet d'établir les conjectures suivantes
Lorsque \(u_0=2\), la suite \((u_n)\) est croissante et sa limite est \(\lim\limits_{n \to +\infty} u_n=6\)
Lorsque \(u_0=11\), la suite \((u_n)\) est décroissante et sa limite est \(\lim\limits_{n \to +\infty} u_n=6\)