Étude d'une suite
Nous allons voir dans cet exercice qu'on peut étudier finement une suite arithmético-géométrique en s'aidant d'une suite géométrique intermédiaire.
Soit \((u_n)\) la suite définie par :
\(u_0=4\)
\(u_{n+1}=2u_n+3\)
et \((v_n)\) la suite définie par \(v_n=u_n+3\)
Question
Écrire un programme sur TI ou Casio permettant de calculer \(u_n\), n étant choisi par l'utilisateur.
Indice
Pour demander à l'utilisateur de saisir une valeur, on utilisera
sur TI :
Prompt Nsur Casio : \("N=" ?→N\)
Indice
Pour effectuer une boucle de 1 à N, on utilisera :
sur TI : For (I,1,N) ... End
sur Casio : For 1→I To N ... Next
Indice
On pourra s'inspirer de l'algorithme[1] utilisé précédemment.
L'affichage de valeur de \(u_n\) peut se faire à la sortie de la boucle car les valeurs intermédiaires ici ne nous intéressent pas.
Solution
Sur TI
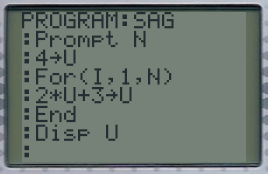
Sur Casio
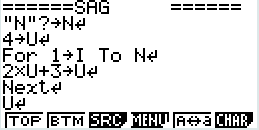
Question
Montrer que la suite \((v_n)\) est géométrique.
En déduire l'expression de \(v_n\) en fonction de n pour tout n
Indice
On pourra exprimer \(v_{n+1}\) en fonction de \(v_n\).
Solution
\(v_{n+1}=u_{n+1}+3=2u_n+3+3=2u_n+6=2(u_n+3)=2v_n\)
On connaît aussi \(v_0=u_0+3=7\).
La suite \((v_n)\) est donc une suite géométrique de premier terme 7 et de raison 2.
On en déduit donc la formule explicite de \(v_n\) en fonction de n :
\(v_n=7\times2^n\)
Question
En déduire une expression de \(u_n\) en fonction de n.
Solution
On sait que \(v_n=u_n+3\) donc \(u_n=v_n-3\).
Or \(v_n=7\times2^n\),
donc \(u_n=7\times2^n-3\).
Question
Étudier les variations de la suite \((u_n)\).
Indice
On pourra s'intéresser au signe de \(u_{n+1}-u_n\).
Solution
\(u_{n+1}-u_n=2u_n+3-u_n=u_n+3=7\times2^n-3+3=7\times2^n\) en utilisant la forme explicite de \(u_n\).
Or \(7\times2^n\) est le produit de nombres positifs. C'est donc un nombre positif pour tout n.
Par conséquent pour tout n, on a \(u_{n+1}-u_n\geq0\).
La suite \((u_n)\) est donc croissante.
Question
Donner la limite éventuelle de la suite \((u_n)\)
Solution
Puisque 2>1, on sait que \(\lim\limits_{n \to +\infty} 2n=+\infty\),
par conséquent on a \(\lim\limits_{n \to +\infty} 7\times2^n=+\infty\).
En retranchant 3, cela donne encore \(\lim\limits_{n \to +\infty} 7\times2^n-3=+\infty\).
On a donc \(\lim\limits_{n \to +\infty} u_n=+\infty\)
Question
Calculer la somme \(u_0+u_1+ ... +u_{10}\).
Indice
On pourra s'aider de la suite \((v_n)\).
Solution
On sait que \(u_n=v_n-3\).
Par conséquent \(u_0+u_1+ ... +u_{10}=v_0-3+v_1-3+ ... +v_10-3=v_0+v_1+ ... +v_{10}-3\times 11\) car on a 11 termes de 0 à 10.
Or on sait calculer \(v_0+v_1+ ... +v_10=v_0\dfrac{1-2^{11}}{1-2}=7\times 2047=14329\).
On en déduit la somme cherchée : \(u_0+u_1+ ... +u_{10}=14329-33=14296\).