Calculs de modules et arguments
Question
Calculer \(|-3+4 i|\)
Solution
\(| -3+4i|=\sqrt{(-3)^2+4^2}=\sqrt{25}=5\).
Question
On donne \(z_A=-1+3i\) l'affixe du point A et \(z_B=2-i\) l'affixe du point B. Calculer la distance AB.
Solution
\(| z_B-z_A|=| 2-i-(-1+3i)| =| 3-4i|=\sqrt{3^2+(-4)^2}=\sqrt{25}=5\).
Donc \(AB=5\).
Question
Calculer \(\arg(2\sqrt 3+2i)\).
Solution
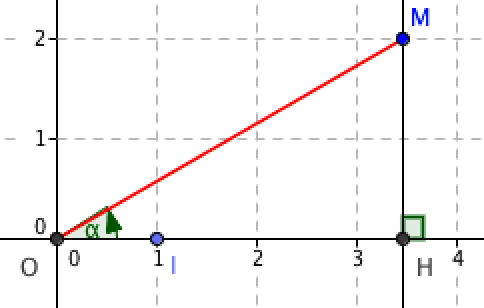
Soit \(\alpha\) la mesure de l'angle \((\overrightarrow{OI} ;\overrightarrow{OM})\), on sait que \(\cos(\alpha)=\dfrac{OH}{OM}\).
\(OM=\sqrt{(2\sqrt3)^2+2^2}=\sqrt{12+4}=\sqrt{16}=4\).
\(\cos \alpha=\dfrac{2\sqrt 3}{4}=\dfrac{\sqrt 3}{2}\).
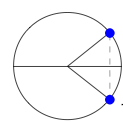
Notre connaissance du cercle trigonométrique nous dit que \(\alpha=\dfrac{\pi}{6}\) ou \(\alpha=-\dfrac{\pi}{6}\).
Mais nous savons de plus que \(\sin \alpha=\dfrac{MH}{OM}=\dfrac{1}{2}\) donc positif.
Cela nous permet d'exclure \(\alpha=-\dfrac{\pi}{6}\).
On conclut que \(\arg(2\sqrt 3+2i)=\dfrac{\pi}{6}~~~(2\pi)\).
Question
Calculer \(\arg(2\sqrt 3-2i)\).
Solution
Soit \(\alpha\) la mesure de l'angle \((\overrightarrow{OI} ;\overrightarrow{OM})\), on sait que \(\cos(\alpha)=\dfrac{OH}{OM}\).
\(OM=\sqrt{(2\sqrt3)^2+2^2}=\sqrt{12+4}=\sqrt{16}=4\).
\(\cos \alpha=\dfrac{2\sqrt 3}{4}=\dfrac{\sqrt 3}{2}\).

Notre connaissance du cercle trigonométrique nous dit que \(\alpha=\dfrac{\pi}{6}\) ou \(\alpha=-\dfrac{\pi}{6}\).
Mais nous savons de plus que \(\sin \alpha=-\dfrac{MH}{OM}=-\dfrac{1}{2}\) donc négatif.
Cela nous permet de conclure \(\alpha=-\dfrac{\pi}{6}\).
On conclut que \(\arg(2\sqrt 3-2i)=-\dfrac{\pi}{6}~~~(2\pi)\).