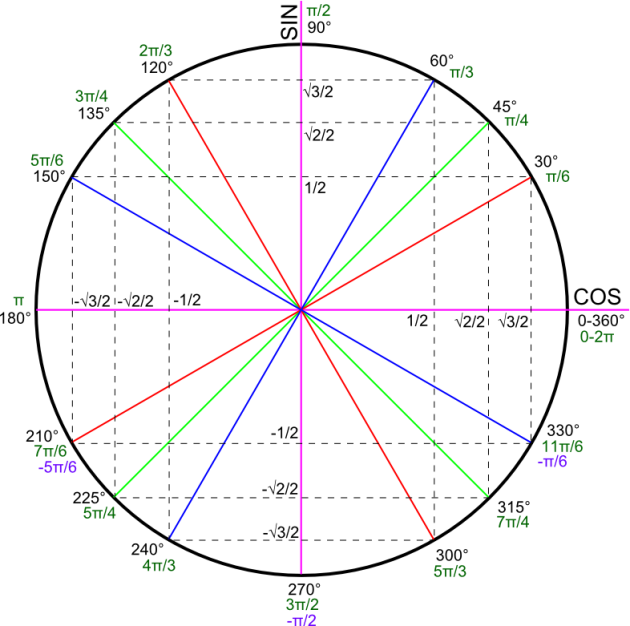
Valeurs particulières
Fondamental : Valeurs remarquables de sin et cos à connaître
\(x\) en degrés | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
\(x\) en radians | 0 | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) |
\(\cos x\) | 1 | \(\frac{\sqrt 3}{2}\) | \(\frac{\sqrt 2}{2}\) | \(\frac{1}{2}\) | 0 |
\(\sin x\) | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt 2}{2}\) | \(\frac{\sqrt 3}{2}\) | 1 |
De ce tableau, et à l'aide du cercle trigonométrique ci-dessus, on déduit aisément les valeurs remarquables de sinus et cosinus pour les angles entre 0 et \(2\pi\) ou entre \(-\pi\) et \(\pi\)
Remarque : Démonstration
Les valeurs du tableau se démontrent facilement par de la géométrie de collège. Nous avons vu précédemment la démonstration de \(cos 60°=\frac{1}{2}\). Le théorème de Pythagore et les symétries permettent de montrer les autres valeurs de cosinus et sinus pour les angles de 30° et 60°
Pour l'angle de 45°, il suffit de savoir que la longueur de la diagonale d'un carré de coté 1 est \(\sqrt 2\)
Dès lors, par simple proportionnalité, la longueur d'un carré dont la diagonale est 1 est \(\frac{1}{\sqrt 2}=\frac{\sqrt 2}{2}\)
coté | 1 | ? ? |
|---|---|---|
diagonale | \(\sqrt 2\) | 1 |