Propriétés des fonctions sin et cos
Fondamental :
Pour tout nombre réel x , on a :
\(-1\leqslant \sin x\leqslant 1\) et \(-1\leqslant \cos x\leqslant 1\)
\(\cos^2 x+\sin^2 x=1\)
\(\sin(-x)=-\sin x\) et \(\cos(-x)=\cos x\)
Remarque : Notation
On note souvent \(\cos^2 x\) pour désigner \((\cos x)^2\) et \(\sin^2 x\) pour \((\sin x)^2\)
Complément : Démonstration des propriétés
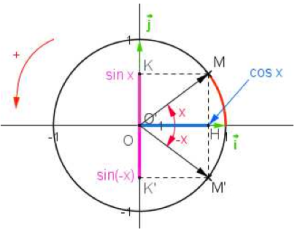
1. La première propriété découle du fait que le sinus et le cosinus sont les coordonnées d'un point du cercle trigonométrique de centre O et de rayon 1. Ces coordonnées sont donc nécessairement comprises entre -1 et 1.
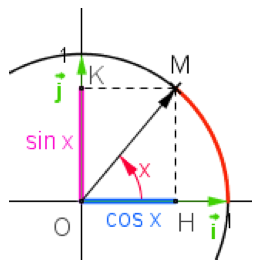
2. La seconde propriété découle de l'utilisation du théorème de Pythagore dans le triangle rectangle OHM, sachant que \(OM^2=1\)
3. Pour la dernière propriété, on remarquera que si un point M correspond à un angle x par enroulement de la droite numérique, l'angle -x revient à faire un enroulement dans le sens contraire et amène à un point M' symétrique de M par rapport à l'axe des abscisses.
Les abscisses de M et M' sont identiques
Les ordonnées de M et M' sont opposées
On en déduit les dernières égalités.