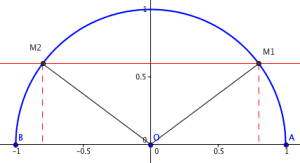
Exemple d'application
Question
Soit x un nombre réel tel que \(\sin x=\frac{3}{5}\)
Calculer \(\cos x\)
Solution
On sait que\( \cos^2 x+\sin^2 x=1\) donc \(\cos^2 x=1-\sin^2 x\)
Par conséquent \(\cos^2 x=1-\dfrac{9}{25}=\frac{16}{25}\)
En se remémorant la résolution des équations carré, on en déduit qu'il y a deux valeurs possibles pour \(\cos x\)
\(\cos x=\frac{4}{5}\) ou \(\cos x=-\frac{4}{5}\)