Vecteurs coplanaires
Définition :
On dit que trois vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires si et seulement si par définition il existe 4 points A,B,C et D d'un même plan tels que :
\(\overrightarrow{u}=\overrightarrow{AB}\), \( \overrightarrow{v}=\overrightarrow{AC}\) et \(\overrightarrow{w}=\overrightarrow{AD}\)
Exemple :
Dans la figure ci-dessous, les vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires. Le vecteur Jaune n'est coplanaire avec aucun couple de deux autres vecteurs.
VectCoplan by wawa on Sketchfab
Le vecteur Jaune n'est coplanaire avec aucun coule de deux autres vecteurs.
Fondamental :
Soient trois vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) tels que \(\overrightarrow{u}\), \(\overrightarrow{v}\) ne sont pas colinéaires.
\(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires si et seulement si
\(\overrightarrow{w}=x\overrightarrow{u}+y\overrightarrow{v}\) avec \(x,y\in \mathbb R\)
Complément : Démonstration
Soient A,B,C et D tels que \(\overrightarrow{u}=\overrightarrow{AB}\),\( \overrightarrow{v}=\overrightarrow{AC}\) et \(\overrightarrow{w}=\overrightarrow{AD}\). Puisque \(\overrightarrow{u}\), \(\overrightarrow{v}\) ne sont pas colinéaires, les points A,B,C définissent un plan dont \((A ;\overrightarrow{u} ;\overrightarrow{v})\) est un repère.
\(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) sont coplanaires, équivaut à dire que A,B,C et D dont dans un même plan et que l'on peut exprimer les coordonnées de D dans le repère \((A ;\overrightarrow{u} ;\overrightarrow{v})\) : \(D(x ;y)\) donc\( \overrightarrow{AD}=x\overrightarrow{u}+y\overrightarrow{v}=\overrightarrow{w}\) ce qui démontre la propriété
Attention :
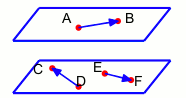
\(\overrightarrow{AB}\), \(\overrightarrow{CD}\) et \(\overrightarrow{EF}\) peuvent être coplanaires sans que les points \(A\),\(B\),\(C\),\(D\),\(E\) et \(F\) soient dans un même plan !
Définition :
Lorsque trois vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) ne sont pas coplanaires, on dit qu'ils sont indépendants ou libres.