Caractérisation d'une droite et d'un plan
Fondamental : Caractérisation d'une droite
Une droite peut être définie par :
un point A et
un vecteur non nul \(\overrightarrow{u}\).
La droite est alors l'ensemble des points M de l'espace vérifiant \(\overrightarrow{AM}=x\overrightarrow{u} ~, ~~x\in \mathbb R\).
On dit que \(\overrightarrow{u}\) est un vecteur directeur de la droite.
Fondamental : Caractérisation d'un plan
Un plan peut être défini par :
un point A et
deux vecteurs non colinéaires \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Le plan est alors l'ensemble des points M de l'espace vérifiant \(\overrightarrow{AM}=x\overrightarrow{u} +y\overrightarrow{v}~, ~~x,y\in \mathbb R\).
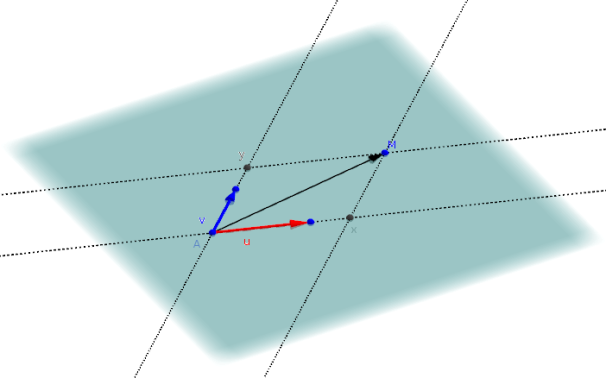
On dit alors que les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) dirigent le plan.
Tout vecteur du plan peut s'écrire comme combinaison \(x\overrightarrow{u} +y\overrightarrow{v}~, ~~x,y\in \mathbb R\).
(A,\(\overrightarrow{u}\), \(\overrightarrow{v}\)) définissent un repère de ce plan. x et y sont les coordonnées de A dans ce repère.
Fondamental : Conséquences
Deux droites sont parallèles si et seulement si leurs vecteurs directeurs sont colinéaires.
Deux plans ayant même couple de vecteurs directeurs sont parallèles.
Une droite (d) et un plan \(\mathcal P\) sont parallèles si et seulement si un vecteur directeur de (d) est un vecteur du plan \(\mathcal P\).